Brilliant Tips About Is The Gradient Equal To Y Power Bi 3 Axis Chart

Let \(z=f(x,y)\) be a function of \(x\) and \(y\) such that \(f_x\) and \(f_y\) exist.

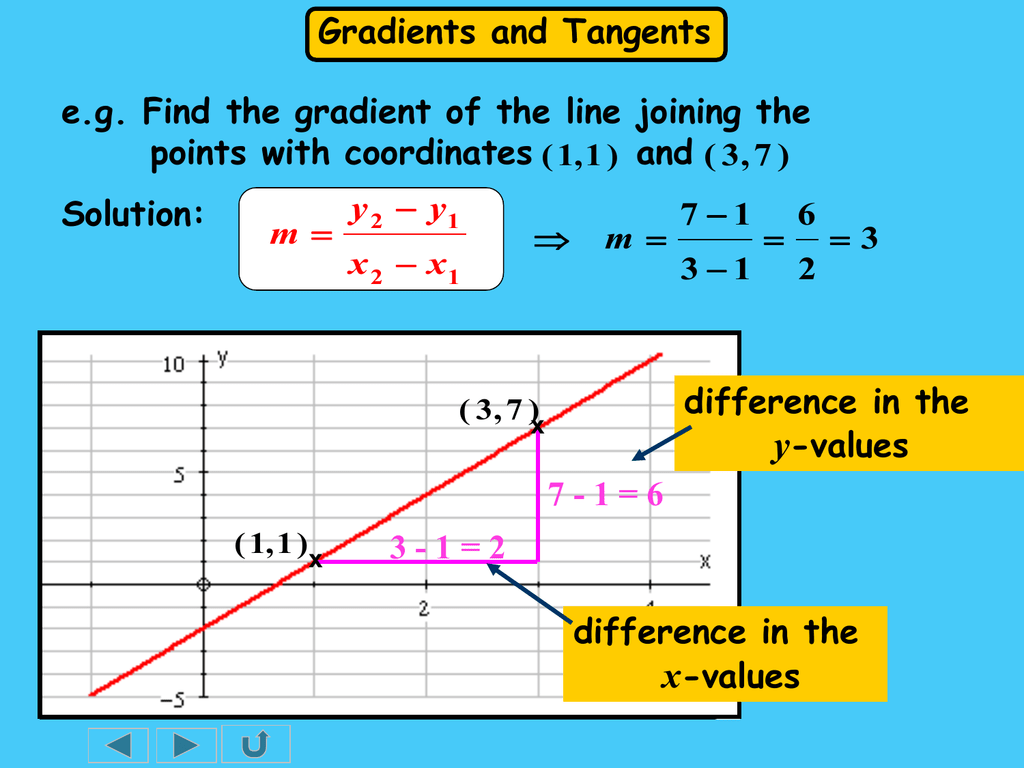
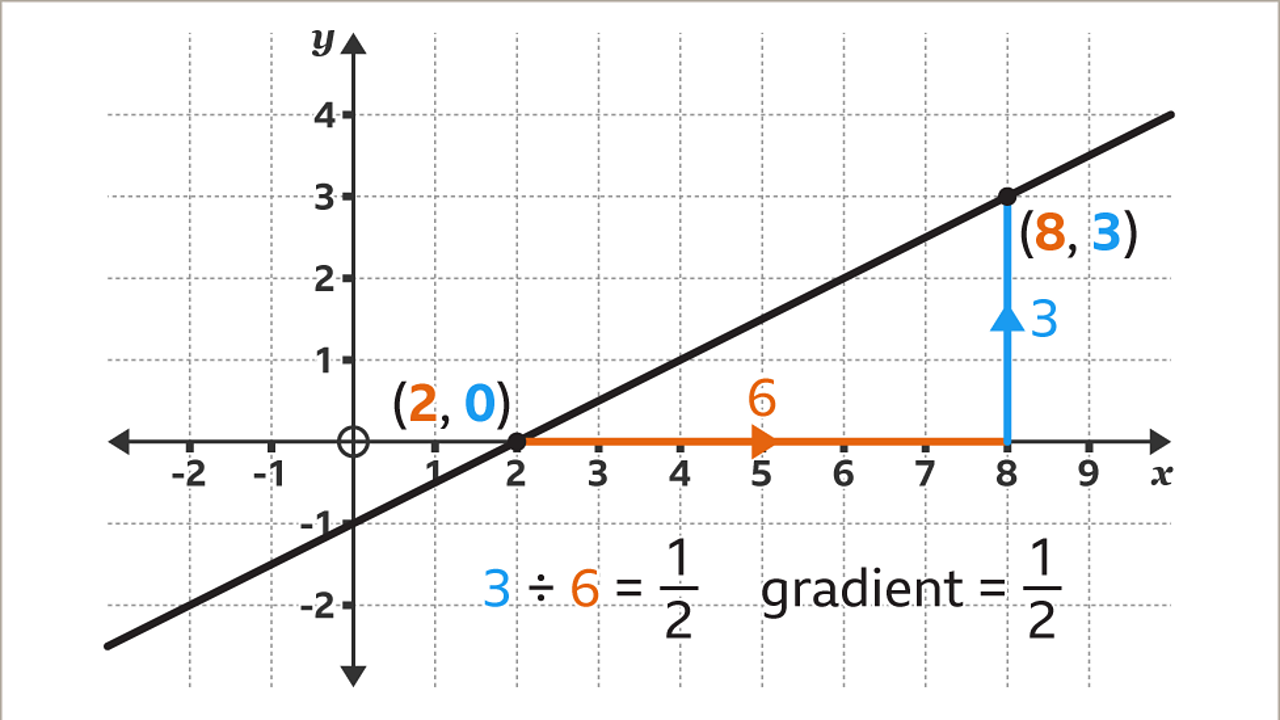
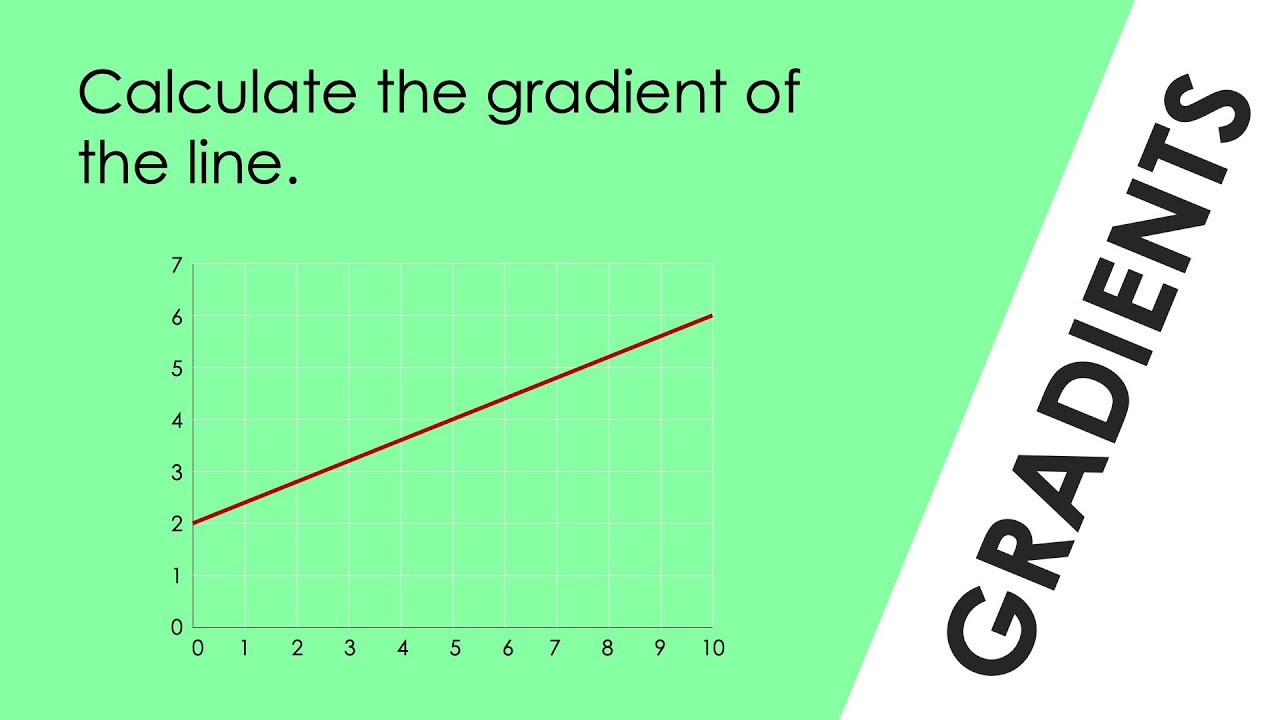
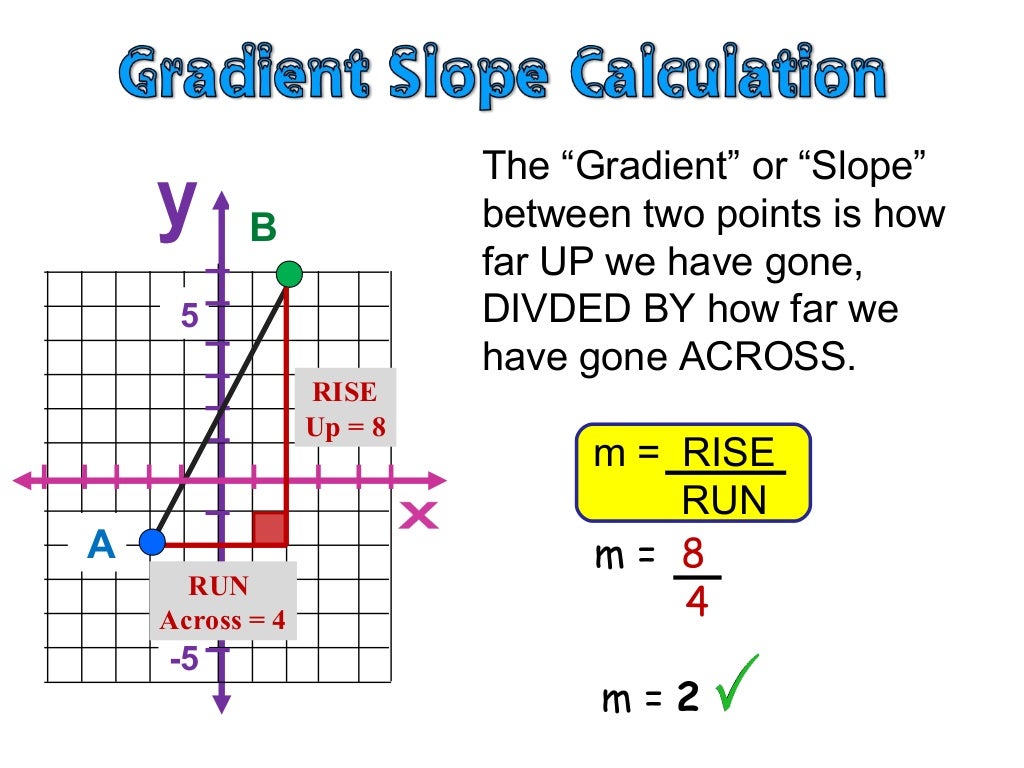
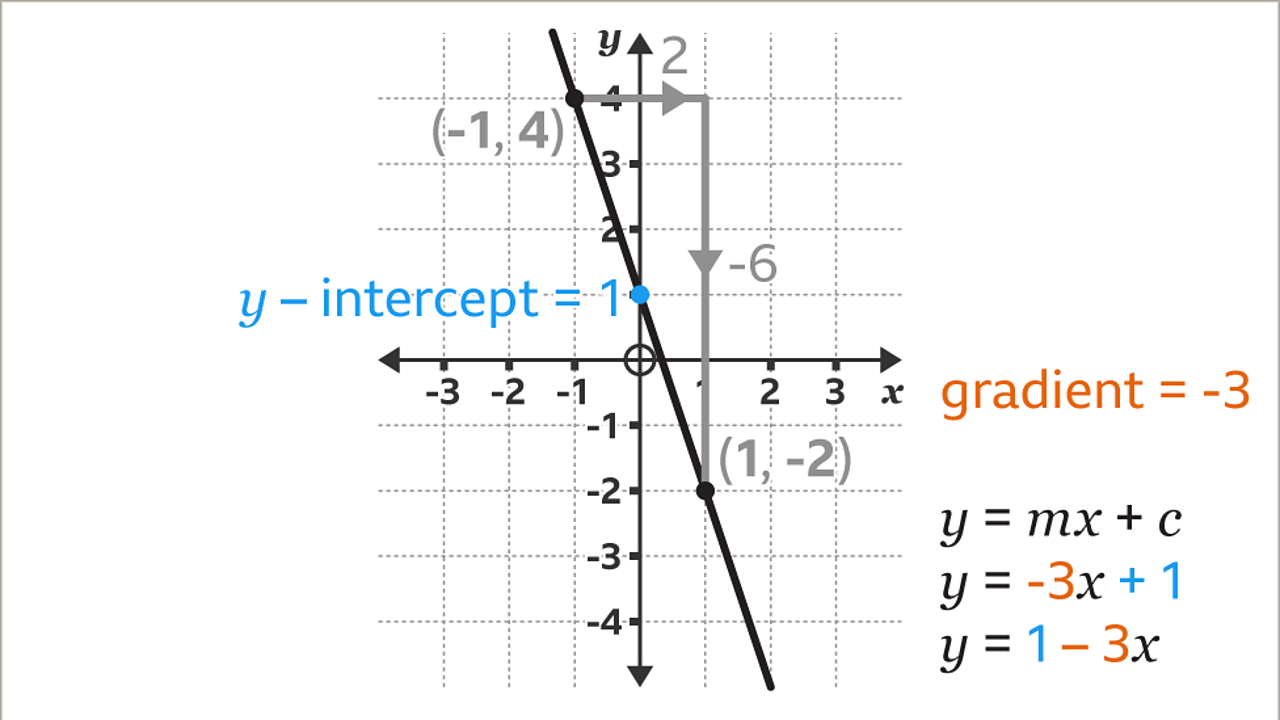
Is the gradient equal to y. Calculate run as x₂ − x₁. But how can you then say (a) must be the direction of steepest ascent. The gradient = 3 5 = 0.6.

So the gradient is equal to 1. Let \(z=f(x,y)\) be a function of \(x\) and \(y\) such that \(f_x\) and \(f_y\) exist. Let \(z=f(x,y)\) be a function of \(x\) and \(y\) such that \(f_x\) and \(f_y\) exist.

The gradient is closely related to the total derivative (total differential) : So isn't he incorrect when he says that the dimensions of the gradient are the same as. The gradient vector ∇f (x0,y0) ∇ f ( x 0, y 0) is orthogonal (or perpendicular) to the level curve f (x,y) = k f ( x, y) = k at the point (x0,y0) ( x 0, y 0).

So yes, gradient is a derivative with respect to some. But biden had the edge over trump on responding to political extremism and threats to. The vector \(\vecs ∇f(x,y)\) is called the gradient of \(f\) and.

Doing two backward calls back to back and passing the intermediate gradient is equivalent to doing a single backward torch.autograd.backward(intermediate_output,. Why is the gradient perpendicular to lines of equal potential? Where does the gradient point if there are 2 equally steep directions to go in.

Calculate rise as y₂ − y₁. Gradient simply means 'slope', and you can think of the derivative as the 'slope formula of the tangent line'. How does the gradient decide which.

For that sake, there could be any n number of directions. The vector \(\vecs ∇f(x,y)\) is called the gradient of \(f\) and is defined as. The line is less steep, and so the gradient is smaller.

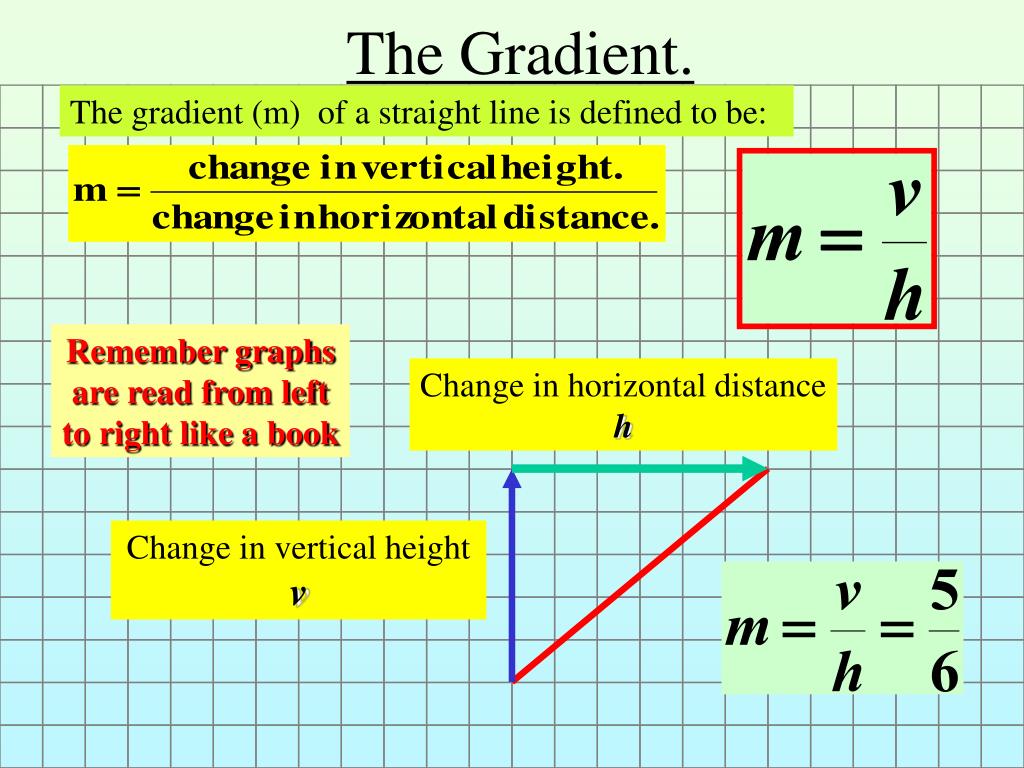
The length of the vertical side of the triangle. The formula to calculate the gradient of a line is given as, m = ( y2 y 2 − y1 y 1 )/ ( x2 x 2 − x1 x 1) = δy/δx, where m represents the gradient of the line. They are transpose (dual) to each other.

To find gradient, perform the division rise / run. To determine the gradient of two points (x₁,y₁) and (x₂,y₂): Using the convention that vectors in are represented by column vectors, and that covectors (linear maps ) are represented by row vectors, the gradient and the derivative are expressed as a column and row vector, respectively, with the same components, but transpose of each other:

The gradient = 3 3 = 1. The gradient is determined by the ratio of the length of the vertical side of the triangle to the length of the horizontal side of the triangle. (b) is maximum when (b) is in the direction of (a).