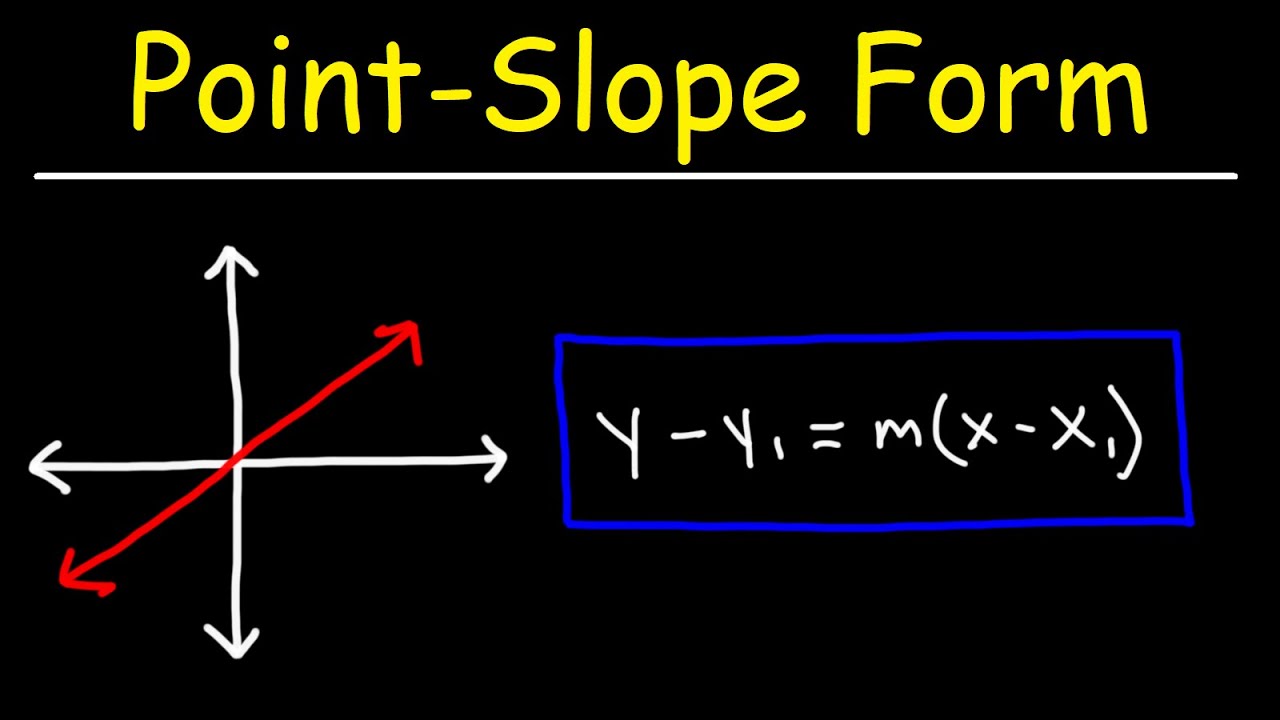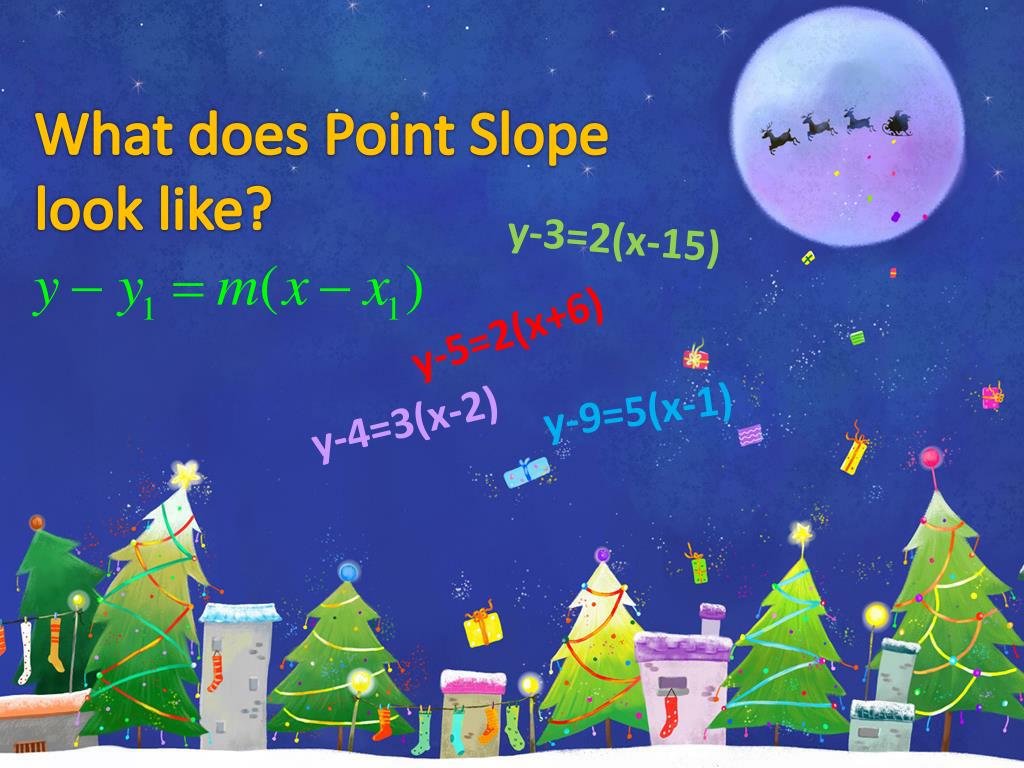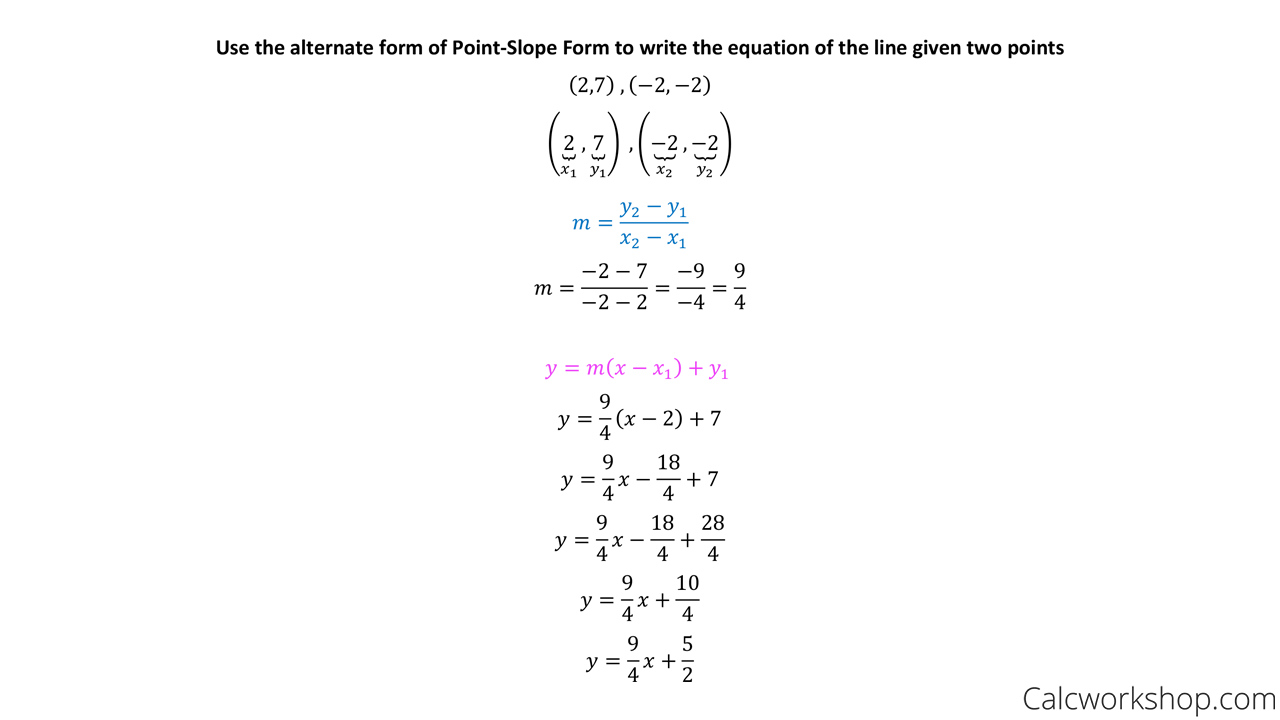The Secret Of Info About What Does Point Slope Look Like Create Graph With Mean And Standard Deviation

It's a standard method for writing the equation of a line.

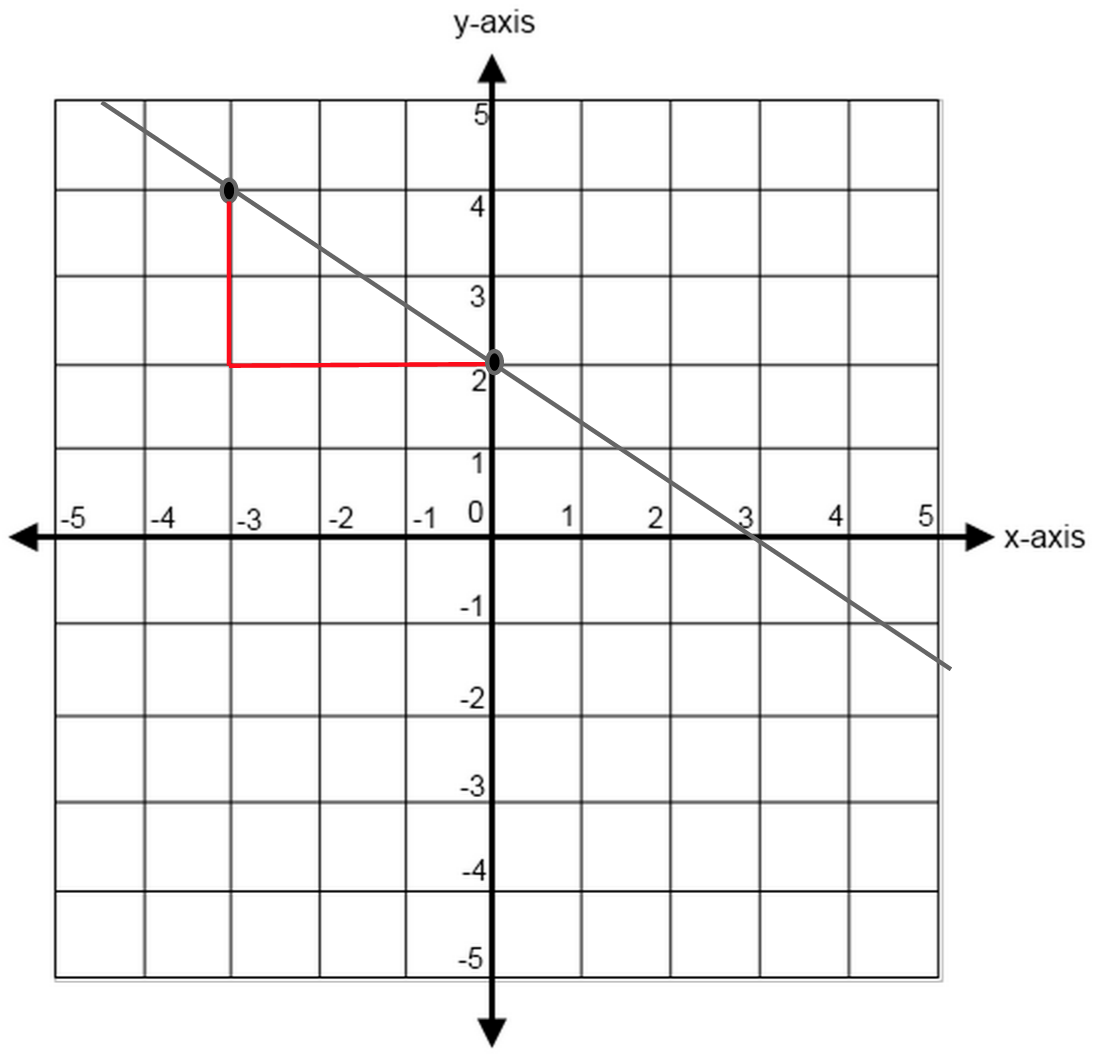
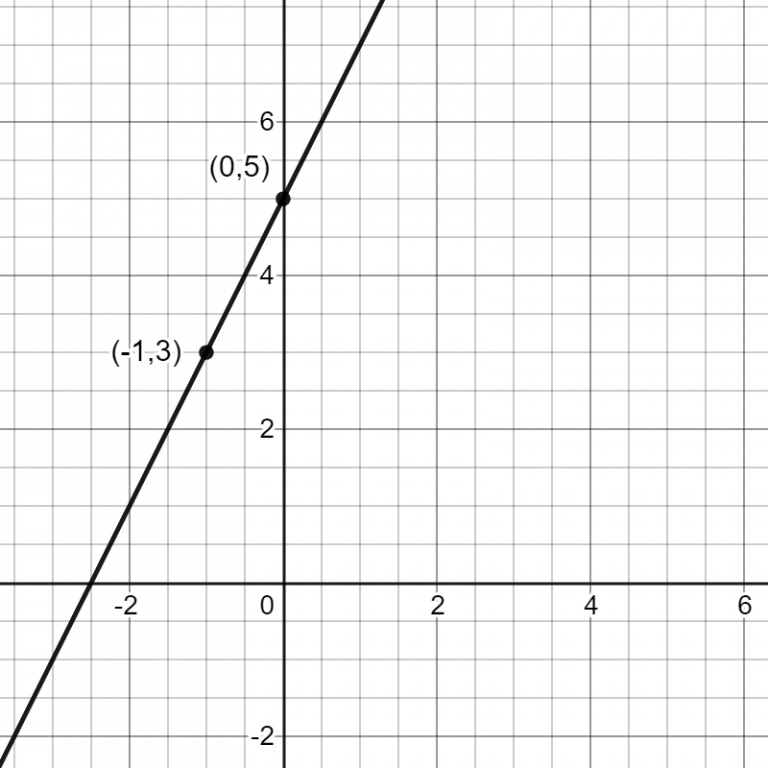
What does point slope look like. This form of the equation is very useful. The line appears to go through the points ( 0, 5) and ( 4, 2). So, it will look like:

In this equation, m is the slope and (x 1, y 1) are the coordinates of a point. Zero slope gives a horizontal line that crosses the x axis at a given y value. Learn point slope formula causing solved examples.

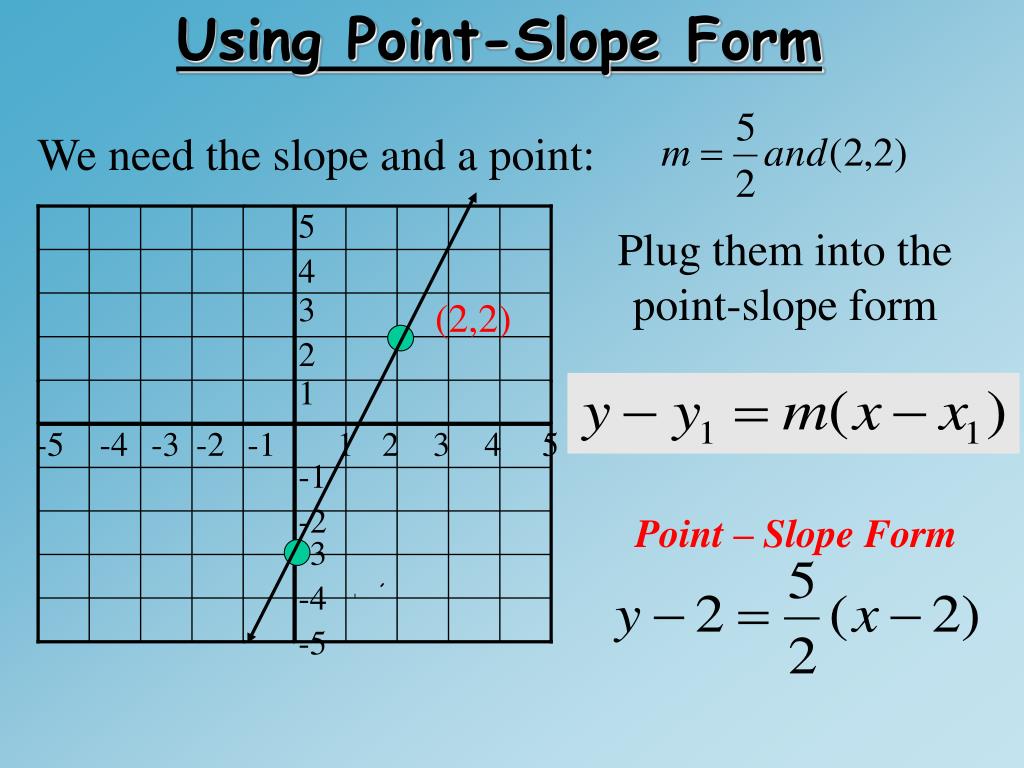
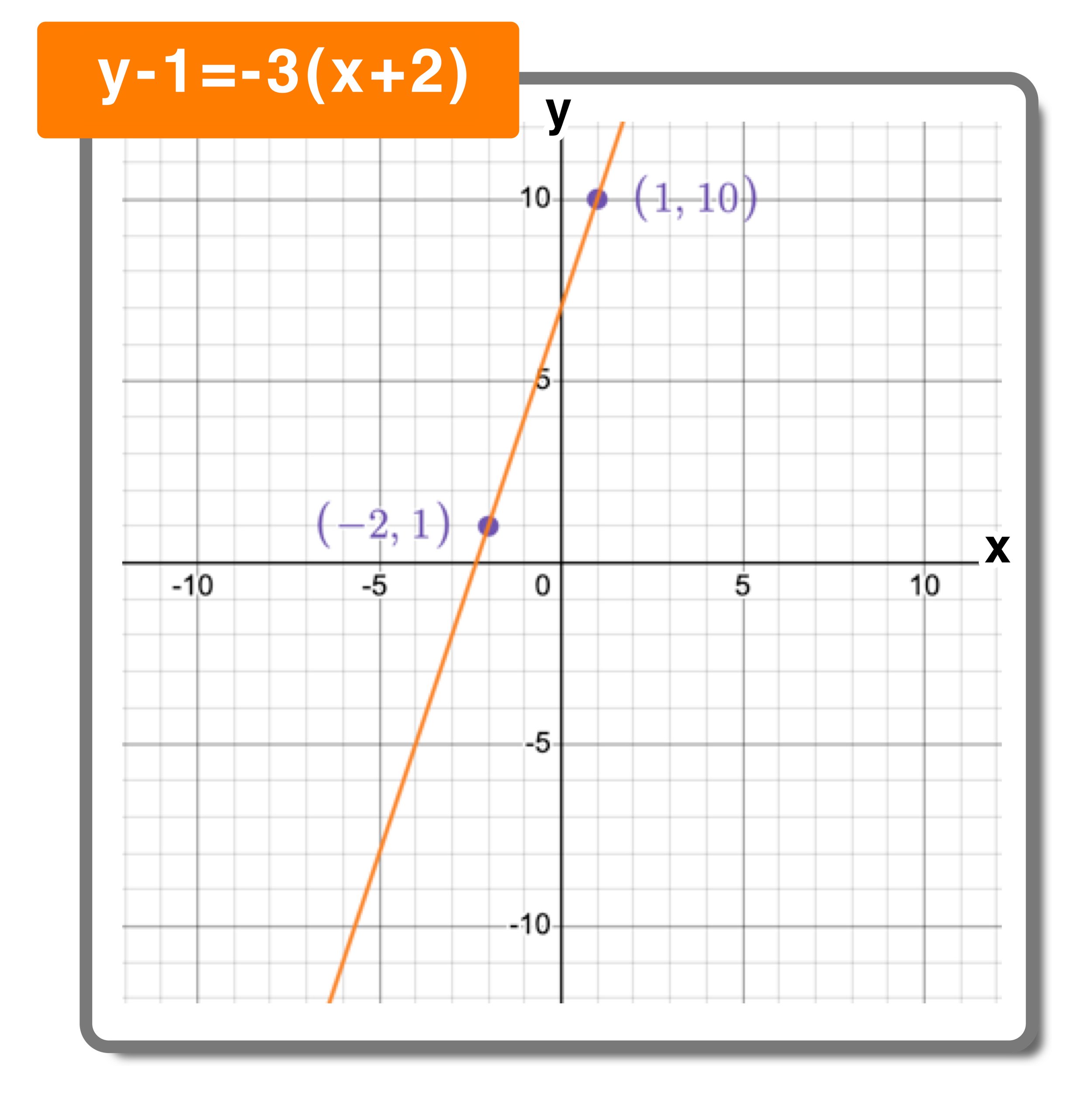
Y − y 1 = m (x − x 1) the equation is useful when we know: Watch this video to learn more about it and see some examples. The equation of the line with slope m that passes through the point \(\left(x_{0}, y_{0}\right)\) is:

Mason miller 34 second mechanical analysis feel free to watch my full mason miller breakdown via yt ( in bio) extension of limbs i really like what he does with his limbs as he enters his. Y = mx + b where m and b are numbers. In other words, for every three units we move vertically down the line, we move four units horizontally to the right.

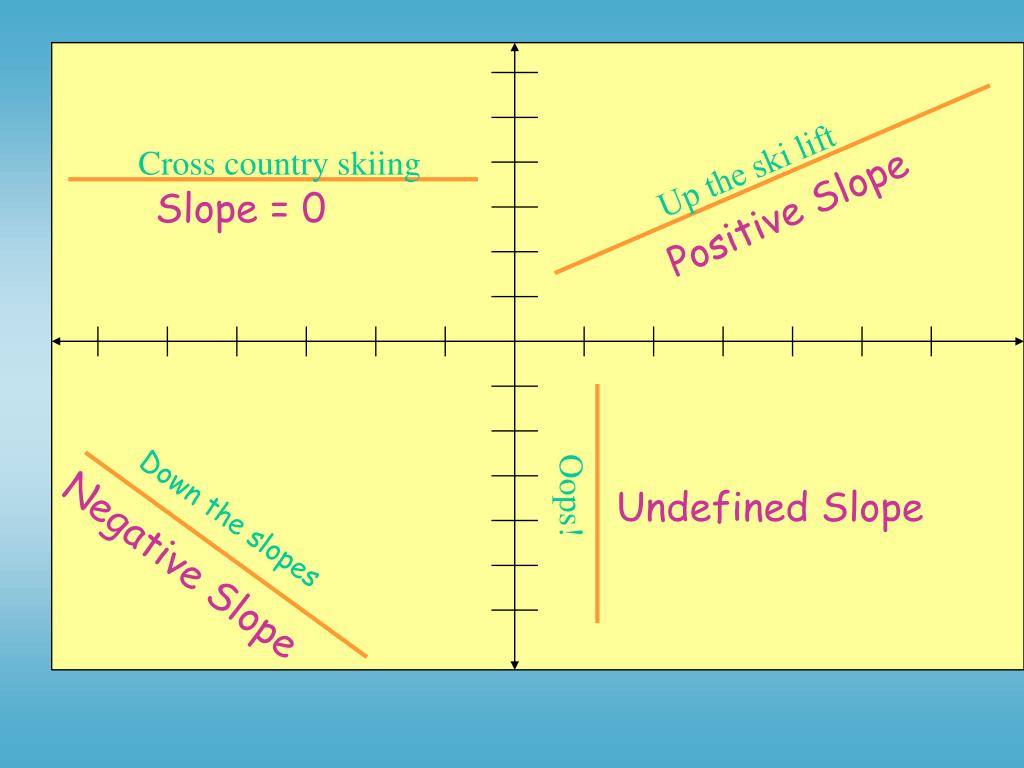
If the orange line looked like this, it now has a positive slope. Y − y1 = m ∗ (x − x1) y − y 1 = m ∗ ( x − x 1) it should be noted that y1 y 1 does not mean y multiplied by 1. What does it look like?

Graph a line given a point and a slope. The variable m is the slope of the line. The point slope form of an equation is directly linked to straight lines in geometry and algebra.

Up is positive, and down is negative. Mathematicians use this form specifically to define the equation of a straight line when they know the slope of the line and at least one point on the line. The coefficient of x (the m value) is the slope of the line.

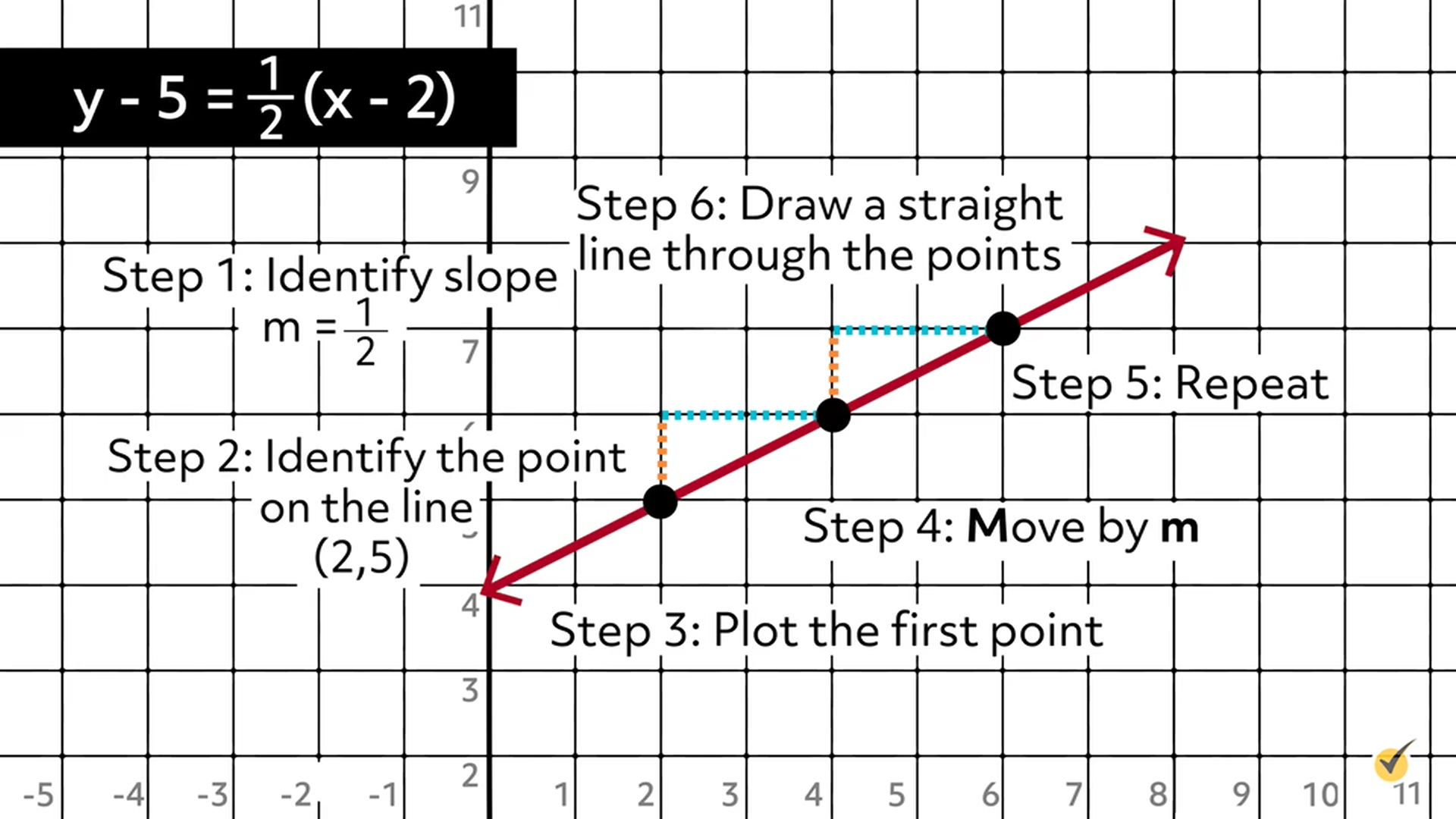
Use the slope formula to identify the rise and the run. That line goes down as you move along, so it has a negative slope. (x1, y1) and the slope of the line:

Starting from the left and going across to the right is positive. It has two variables, x and y, and an unlimited number of solutions (the line is infinitely long). Starting at the given point, count out the rise and run to mark the second point.

Y − b = m ( x − a) when an equation is written in this form, m gives the slope of the line and ( a, b) is a point the line passes through. In this case it denotes a specific y value which you will plug into the equation. Technically speaking, it has three forms: