Recommendation Tips About Can A Linear Model Be Curved Node Red Line Chart Example

Linear regression is a very powerful statistical technique as it can be used to describe more complicated functions (such as exponential or power functions) by linearizing the data sets in question.

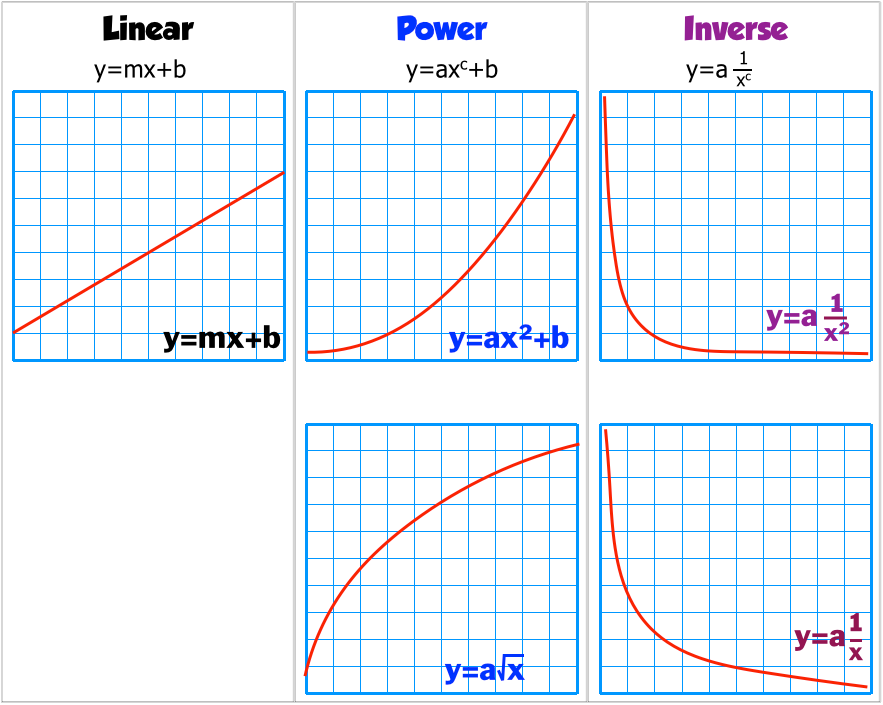
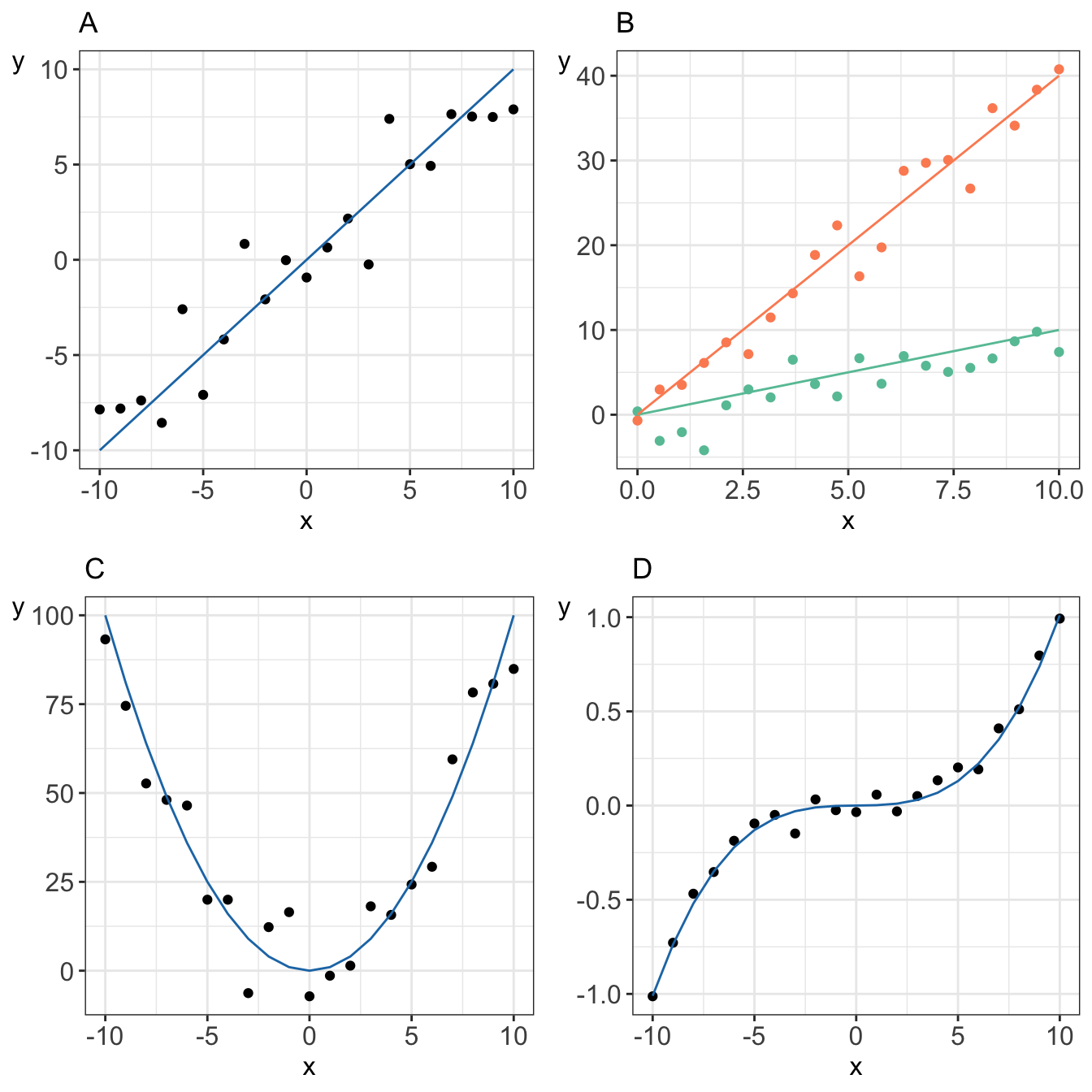
Can a linear model be curved. Common examples of curvilinear regression models include: While linear regression can model curves, it is relatively restricted in the shapes of the curves that it can fit. While the formula must be linear in the parameters, you can raise an independent variable by an exponent to model curvature.

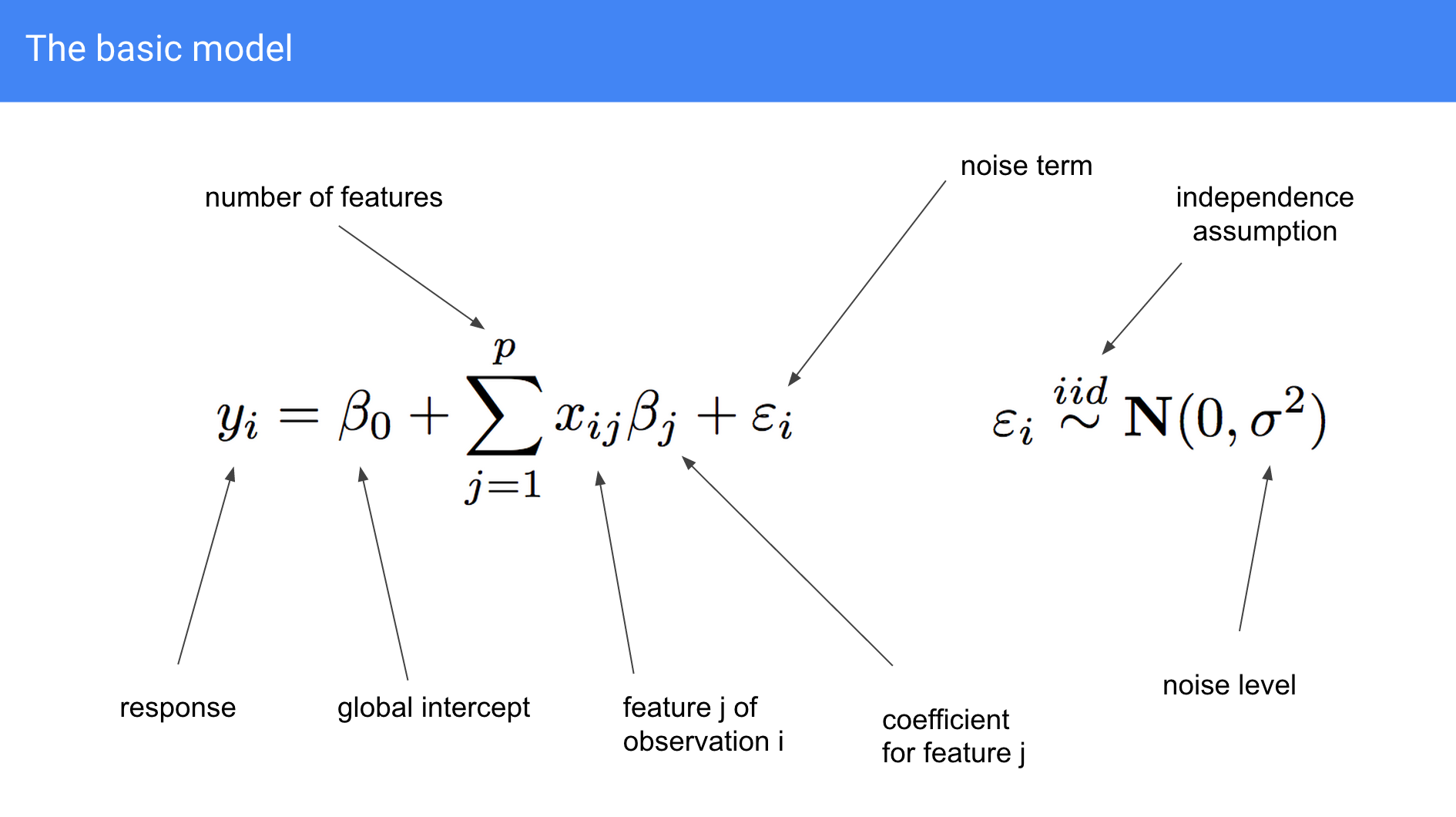
Polynomial terms are independent variables that you raise to a #0excludeglossary, such as squared or cubed terms. The linear regression model has a form like this: You can model some “curves” in your data using, say, variable x and variable x^2 (x squared) as predictors.

While the function must be linear in the parameters, you can raise an independent variable by an exponent to fit a curve. However, despite the name linear regression, it can model curvature. Typically, you choose the model order by the number of.

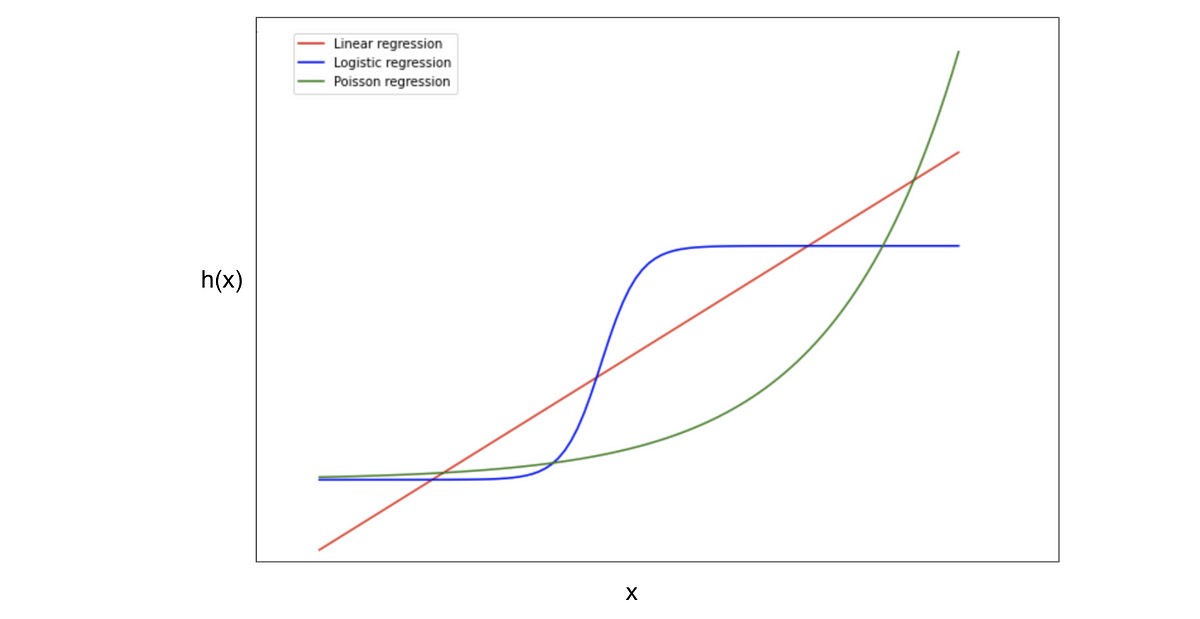
Used when a quadratic relationship exists between a predictor variable and a response variable. Linear regression models use a straight line, while logistic and nonlinear regression models use a curved line. When your variables are not linearly related, try transforming your data.

2/x + 1/y = 3 2 / x + 1 / y = 3. The graphs below illustrate this with a linear model that contains a cubed predictor. The most common method is to include polynomial terms in the linear model.

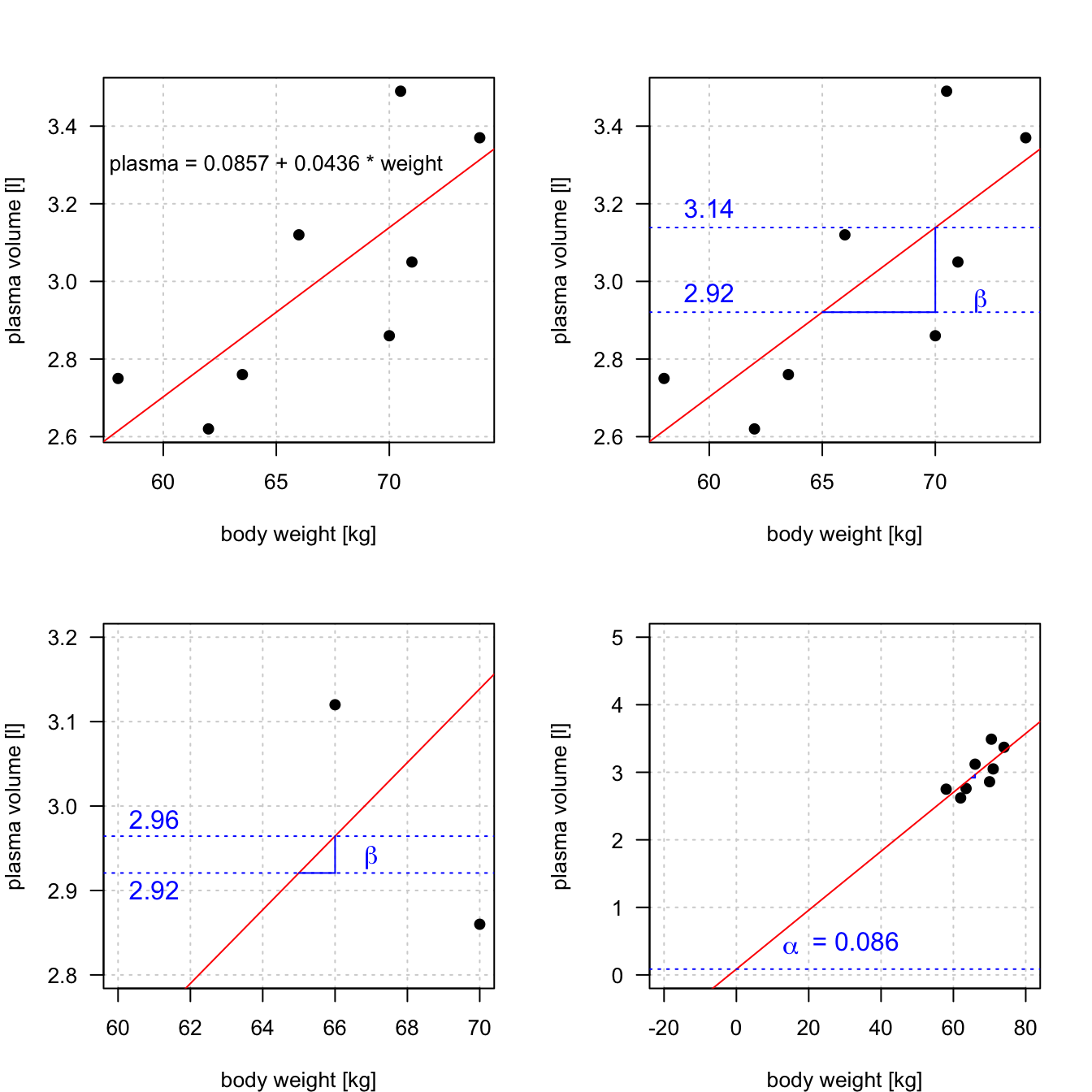
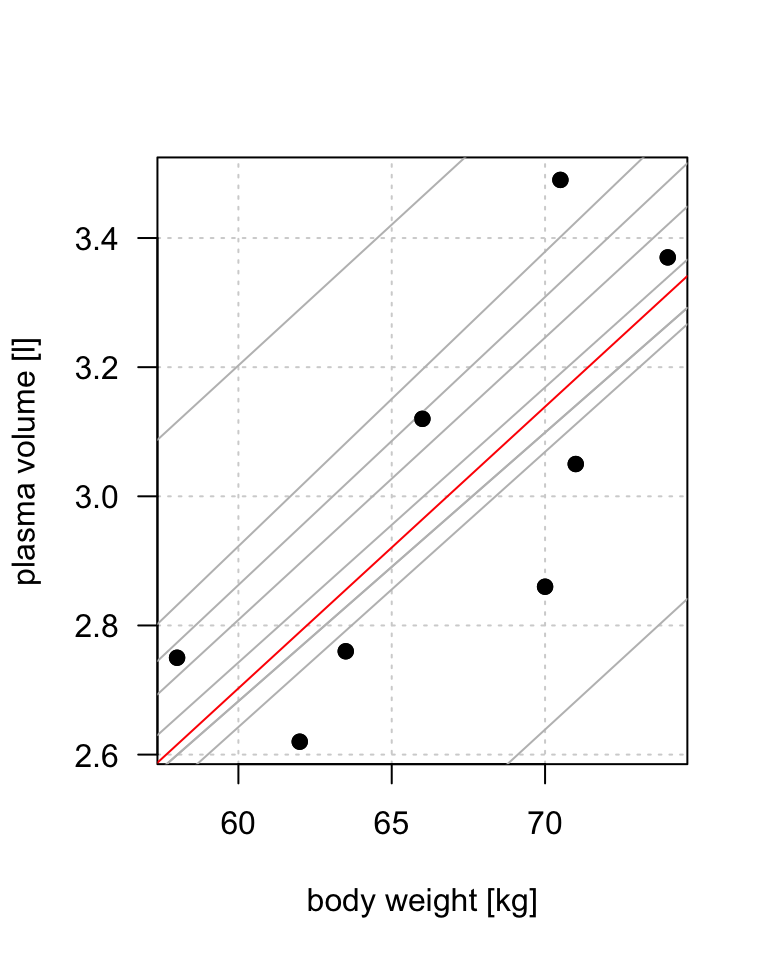
While the equation must be linear in the parameters, you can transform the predictor variables in ways that produce curvature. These data are from an introductory physics experiment. Y' = a+b 1 x 1 + b 2 x 2.

A linear model is not useful in this nonlinear case. It's a line with 1 iv, a plane with 2 ivs, and a hyperplane with 3 or more ivs. Y = b o + b 1 x 1 + b 2 x 12.

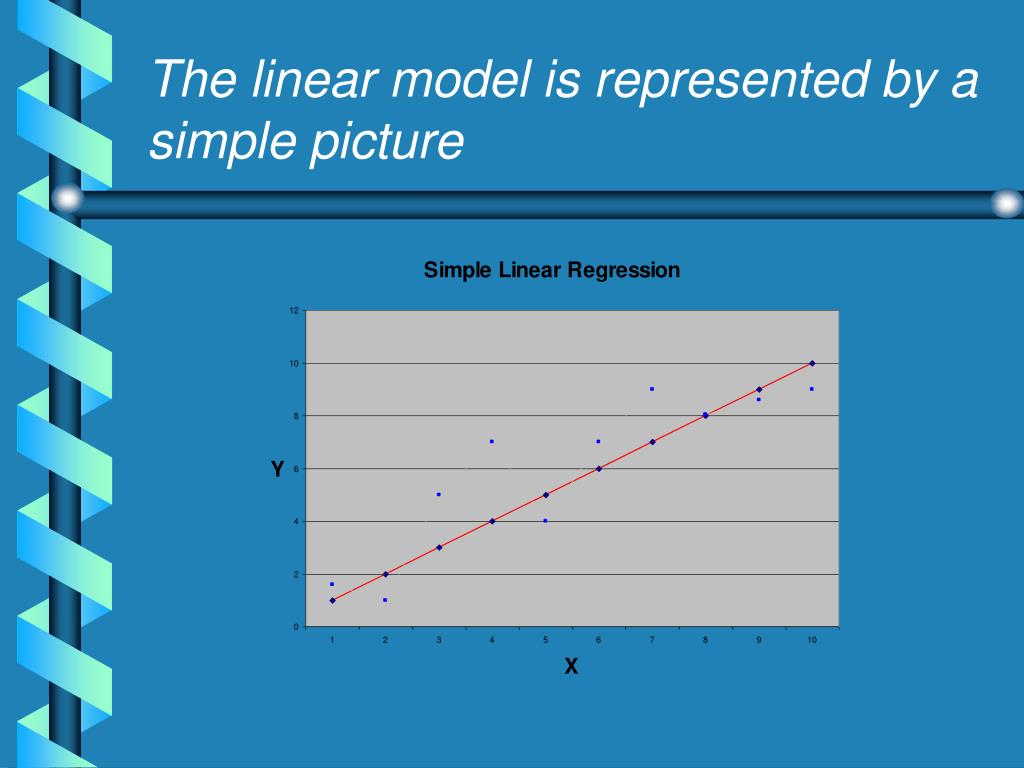
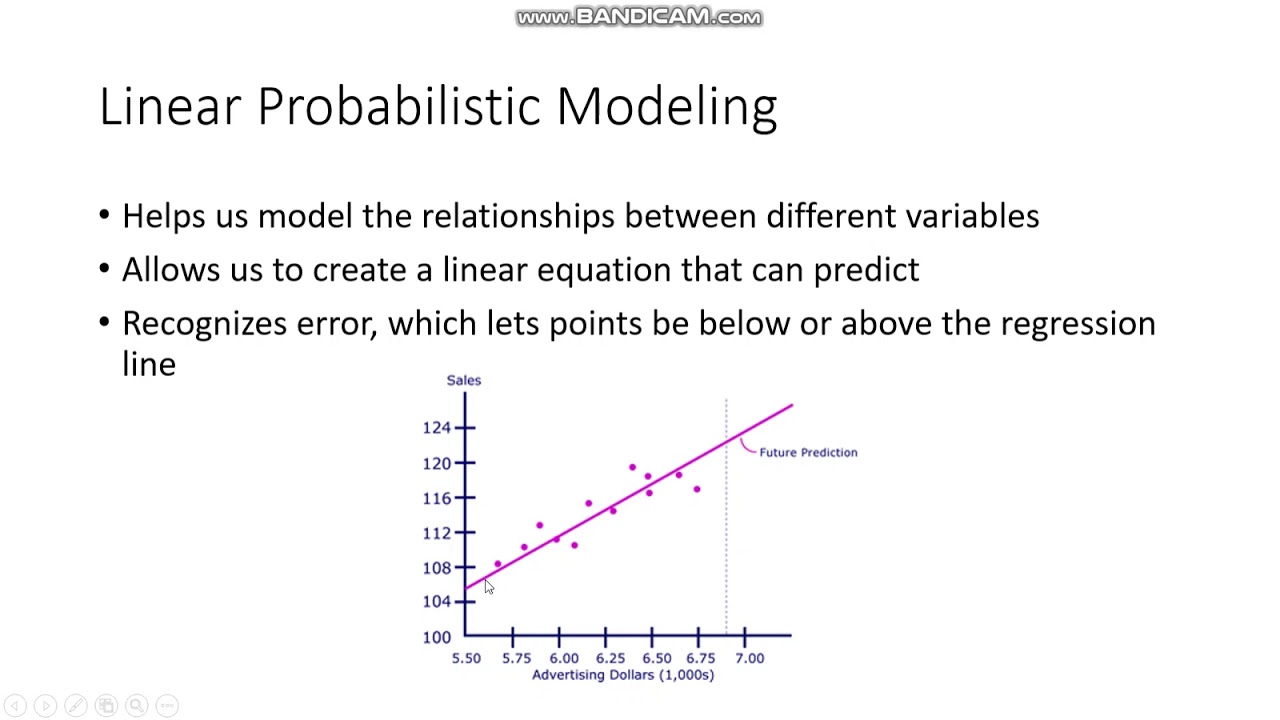
In this sense it is still linear while in essence it is a polynomial curve. In practice, a line is often not an adequate model. If your variables appear to be related linearly, use a simple linear regression model.

Curvilinear regression is the name given to any regression model that attempts to fit a curve as opposed to a straight line. You can choose one or more curve estimation regression models. The void between the simple linear model and the complex trend in data can be filled using the polynomialfeatures class present in sklearn.preprocessing.

Otherwise we have to resort to iterative methods (see nonlinear optimization). You can use substitution to turn curved systems into linear systems. But if we can choose a model that is linear, we can leverage the power of linear algebra;