Fine Beautiful Tips About What Is The Concept Of Curve Sketching How To Draw Graph In Excel

We want the graph to be qualitatively correct, but not necessarily to scale.

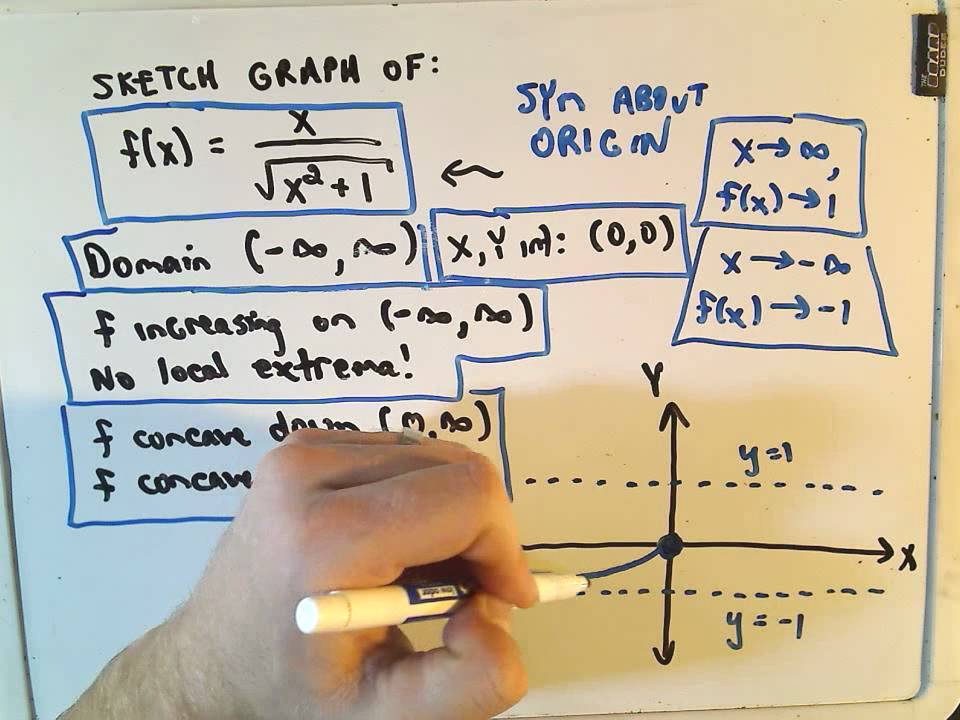
What is the concept of curve sketching. In figure \ (\pageindex {2c}\) we show a graph of \ (f\) drawn with a computer program, verifying the accuracy of our sketch. The next theorem is almost the converse of the first shape theorem and explains the relationship between the values of the derivative and the graph of a function from a different perspective. But some of the steps are closely related.

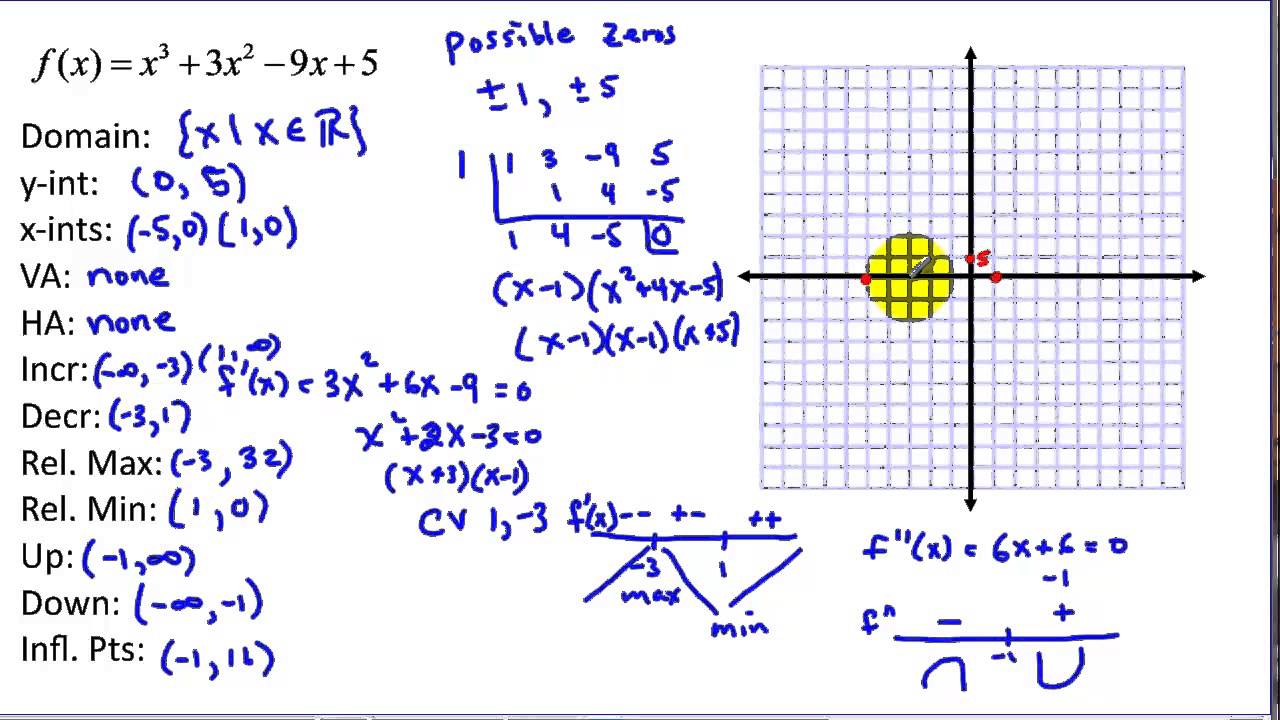
Find the domain of the function and determine the points of discontinuity (if any). We can make a fairly accurate sketch of any function using the concepts covered in this tutorial. Sketching curves of functions and their derivatives.

Derivatives are key in identifying slopes and concavity, aiding in a systematic approach to sketching curves. By drawing these graphs, you can interpret how functions behave, which can be indispensable in solving engineering problems. Applying derivatives to analyze functions.

To draw the graph of f using information about whether f and f are positive or negative. Increasing and decreasing functions. Approximation and curve sketching part b:

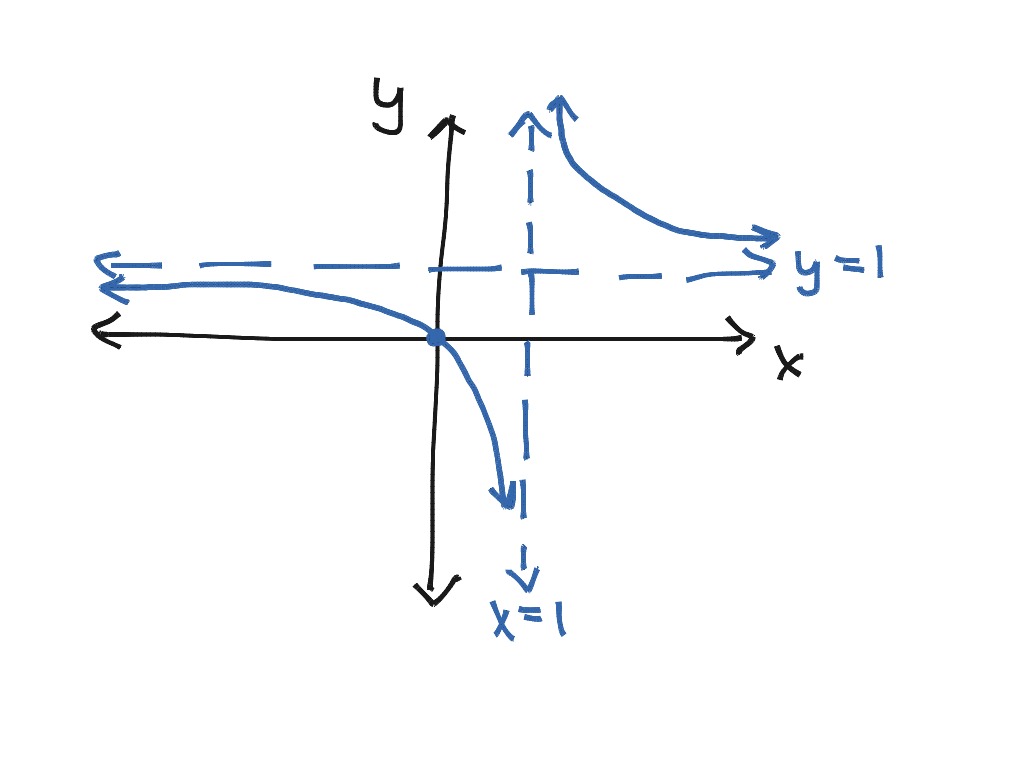
Introduction to curve sketching. Sometimes these are easy to nd, and sometimes it is impossible. F(x) has a denominator, the domain rejects all numbers x where the denominator is zero.

Functions and their graphs are important not only in math but in other fields and applications as well. Notice in this definition that \(x\) and \(y\) are used in two ways. To find the domain, zeros, and intervals of positivity and negativity.

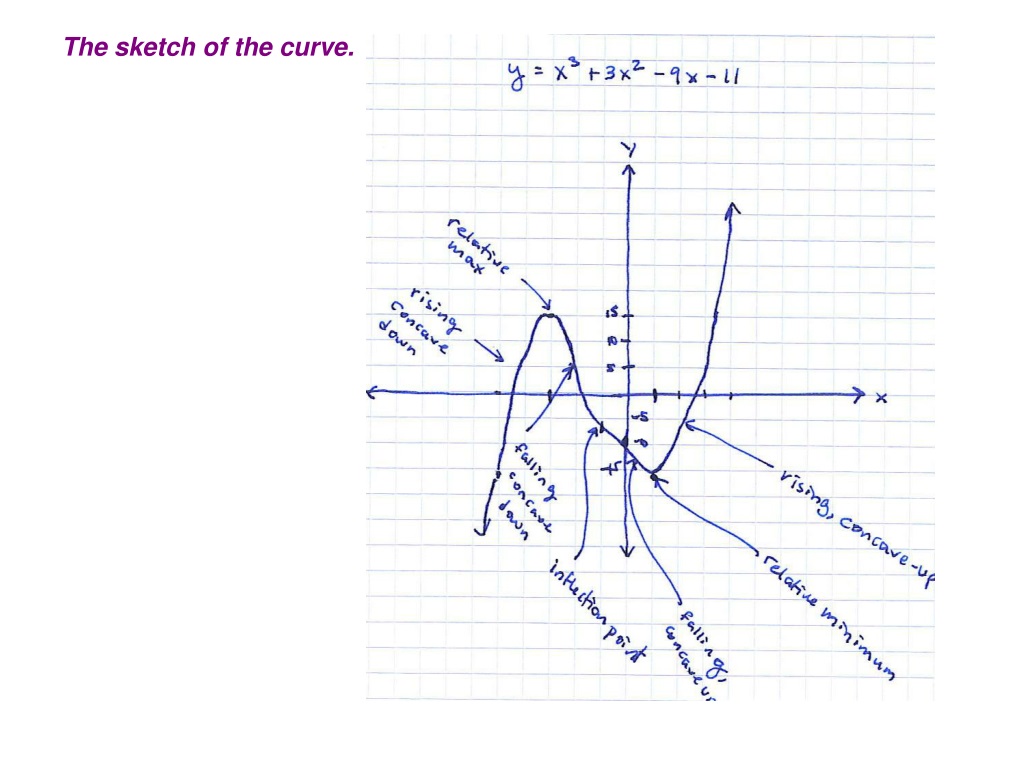
Root, the domain rejects all numbers x where what's i. A function f is decreasing on an interval (a, b) if for any two numbers x1 and x2 in (a, b), f(x1) > f(x2) whenever x1 < x2. Curve sketching shows us how we can understand and predict the behavior of the function based on its first and second derivatives.

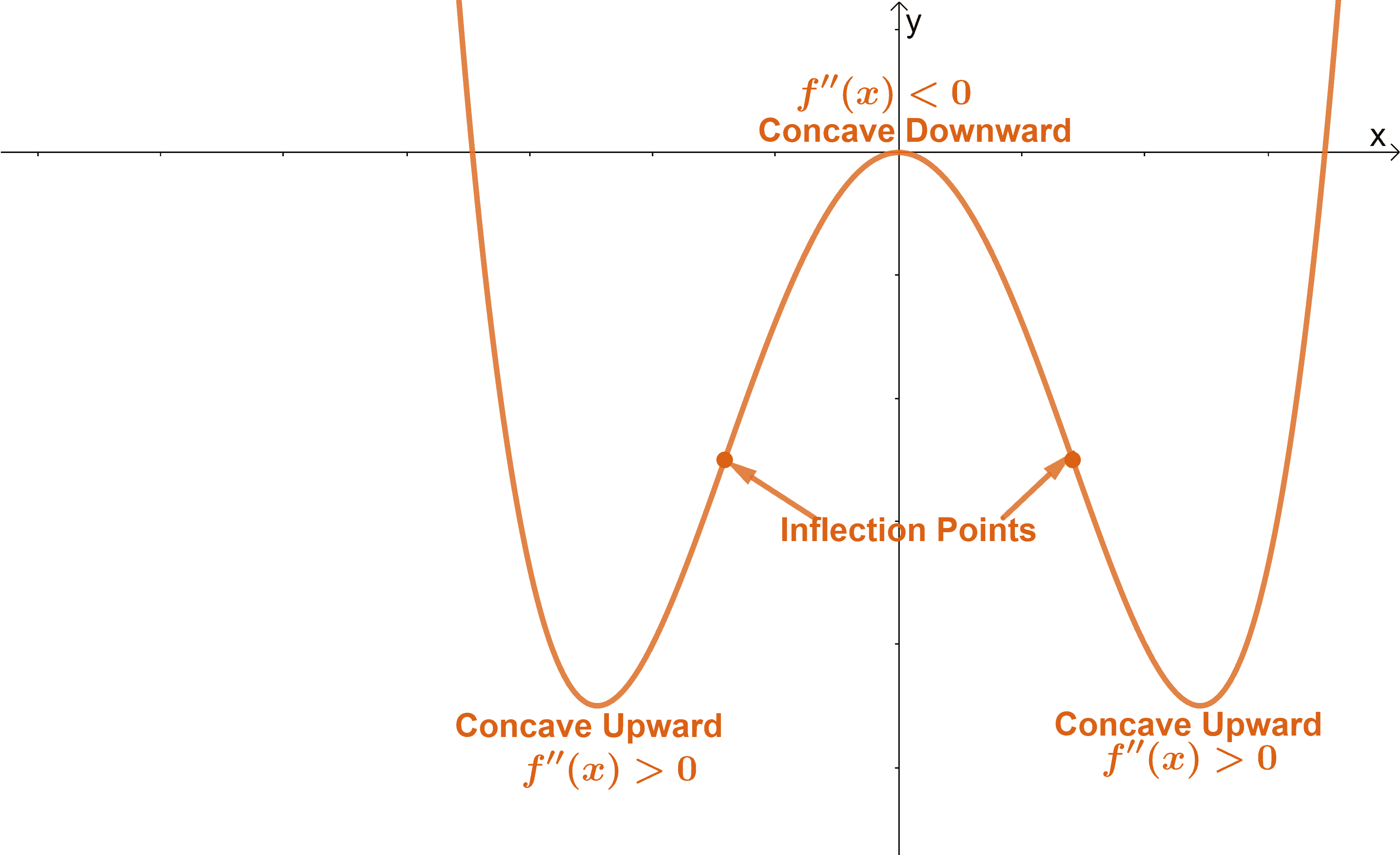
The second derivative test further refines this analysis. It involves analyzing intercepts, turning points, symmetry, and asymptotes. Sketching \ (f\) in example \ (\pageindex {1}\).

Using this information, we can sketch a graph of \(v(t) = \frac{dh}{dt}\). O the equation f(x) = 0. Using local minima and maxima, concavity and inflection points, and where a function increases or decreases, you can sketch the graph of a function.

It is an application of the theory of curves to find their main features. A function f is increasing on an interval (a, b) if for any two numbers x1 and x2 in (a, b), f(x1) < f(x2) whenever x1 < x2. Roughly speaking, given a function de ned by a formula, we want to produce its sketch.