Divine Tips About What Function Is A Smooth Curve Create Trend Chart In Excel
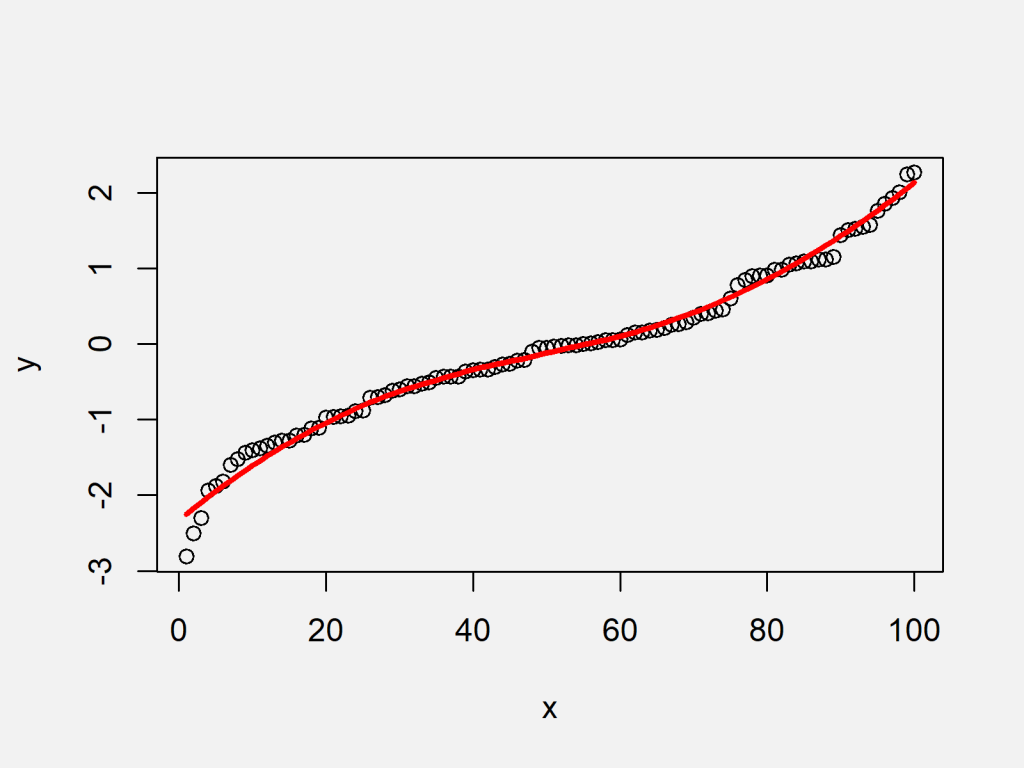
In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise.
What function is a smooth curve. A clear definition of smoothing of a 1d signal from scipy cookbook shows you how it works. When the curvature of a regular curve $\gamma (t)$ is everywhere $>0$, then show that the curvature is a smooth function of $t$. The curve α(t) = (t3, t2) in the plane fails to be.
Yy = smooth(y,method) smooths the data in y using the method specified by method and the default span. For this, one has to clarify whether the curve is considered in the. A curve is said to be smooth if it has no singular points, in other words if it has a (unique) tangent at all points.
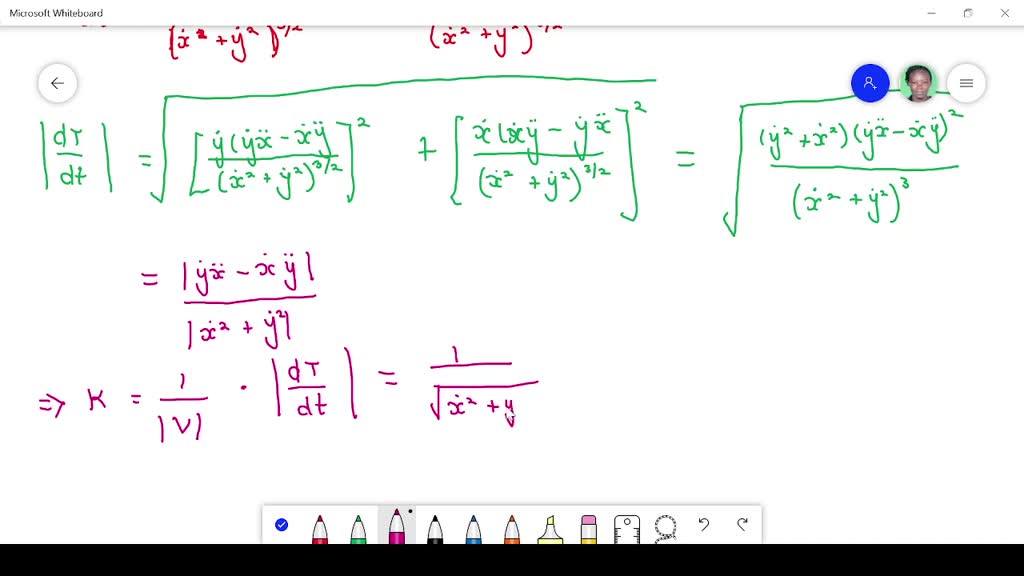
In this section we want to briefly discuss the curvature of a smooth curve (recall that for a smooth curve we require →r ′(t) r → ′ ( t) is continuous and →r ′(t) ≠ 0 r. In the early days of design, a smooth curve was manually drawn through a given set of points by placing metal weights, called “ducks,” at the data points, and then passing a. Consider the following curve in the plane, $(x(t),y(t))$, this curve is called smooth if the functions $x(t)$ and $y(t)$ are smooth, which simply means that for all $n$, the.
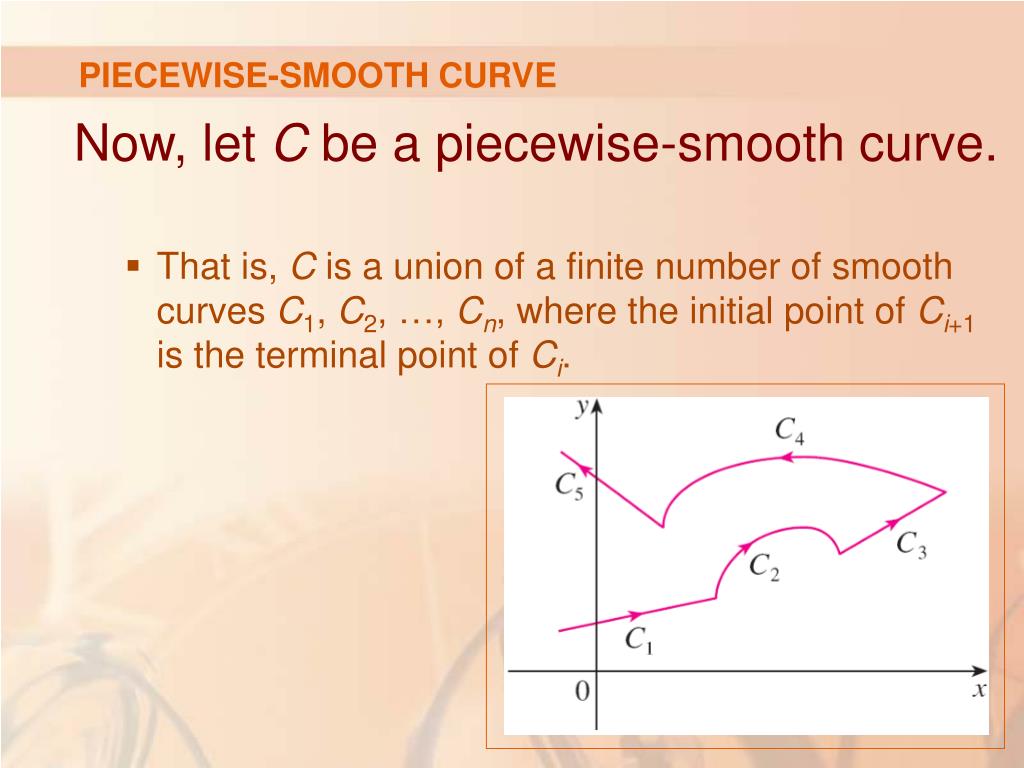
I → r3 is said to be regular if α'(t) ≠ 0 for all t ∊ i. Equivalently, we say that α is an immersion of i into r3. The notions of curves in the complex plane that are smooth, piecewise smooth, simple, closed, and simple closed are easily formulated in terms of the vector function (1).
Note that the formulas are defined for smooth curves: A smooth curve is a curve which is a smooth function, where the word curve is interpreted in the analytic geometry context. A curve $\gamma\colon i \to \mathbb{r}^n$ is smooth iff it is $c^\infty$ (or $c^p$ for some authors).
Yy = smooth(y,span) sets the span of the moving average to span. Finally, based on completely adjusting the model, we performed smooth curve fitting and explored the relationship between wc and lung function parameters. A function can therefore be said to be smooth over.
A function can therefore be said to be smooth over. A smooth function is a function that has continuous derivatives up to some desired order over some domain. Let's define a wavy function:
If $a \in s$ and. Could you give me some hints how we could. And add lots of noise:
So by the inverse function theorem, the level sets of $f(x,y)$, which are just the inverse images of sets $x = c$ under the map $f(x,y)$, are smooth near $(x_0,y_0)$. A smooth function is a function that has continuous derivatives up to some desired order over some domain.
![[Math] Smooth curve and smooth surface Math Solves Everything](https://i.stack.imgur.com/28xcj.png)
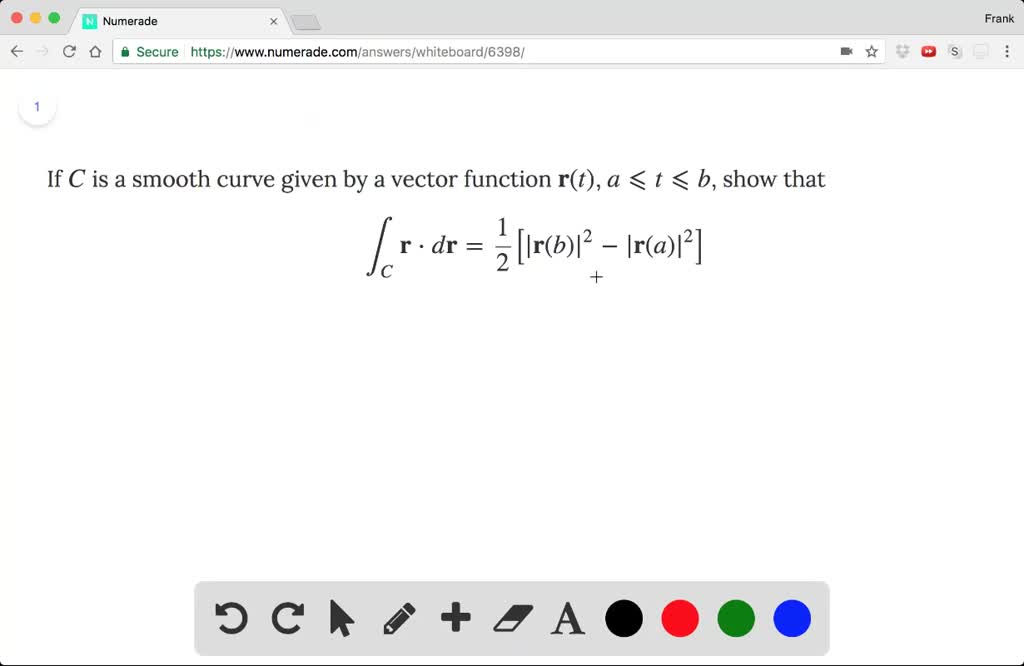


![[Math] Smoothing of a step function using smoothstep. (Curve fitting](https://i.stack.imgur.com/4zBDR.jpg)










![[Tex/LaTex] Tangent Lines Diagram Along Smooth Curve Math Solves](https://i.stack.imgur.com/vkUwe.png)