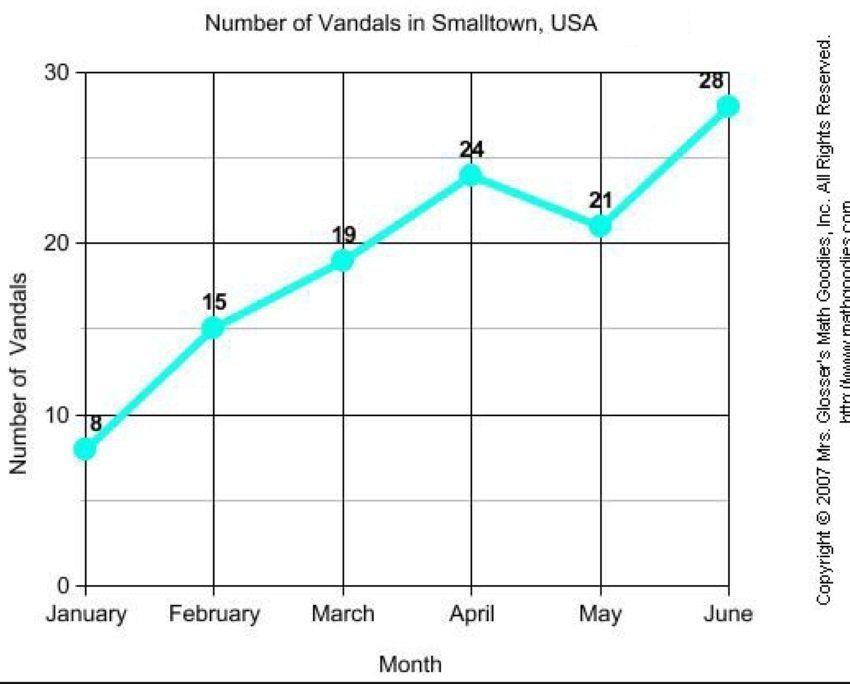
Cool Info About How To Determine If A Graph Is Simple Make Trend Line

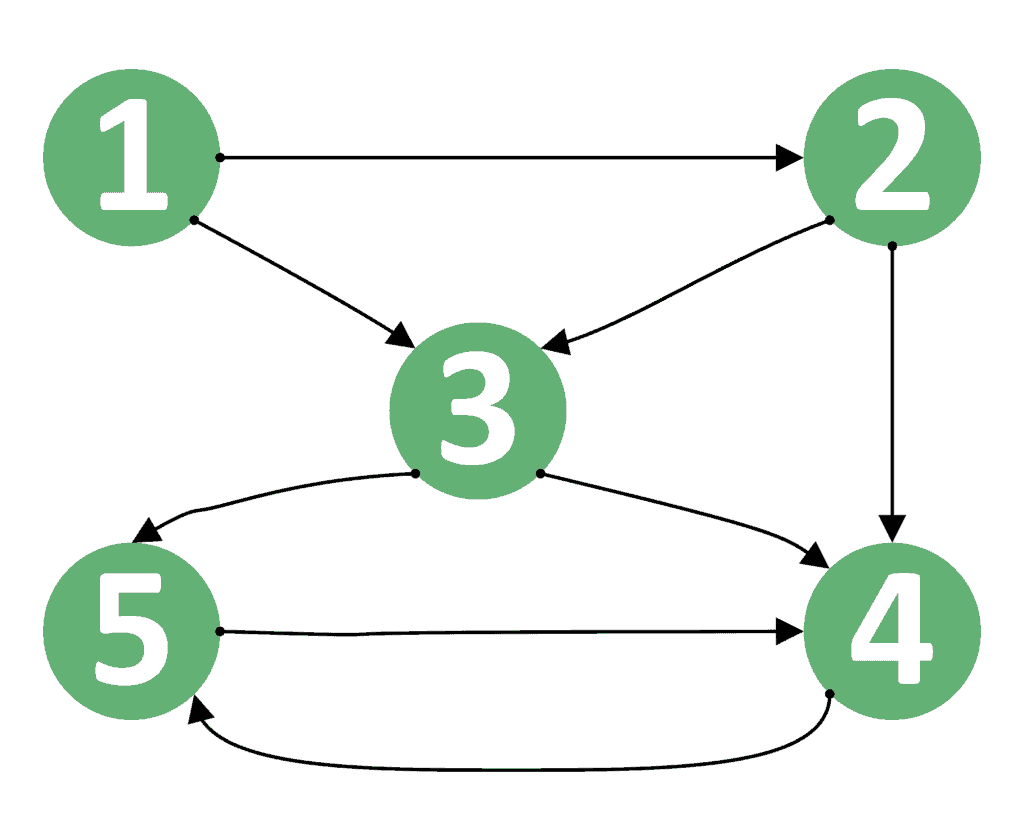
If the graph is simple, and $\deg v_1=3$, $v_1$ must be adjacent to each of the other three vertices.

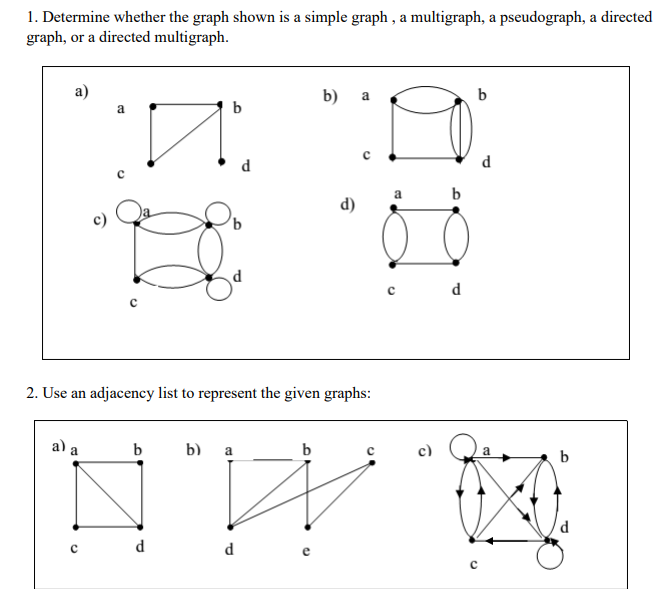
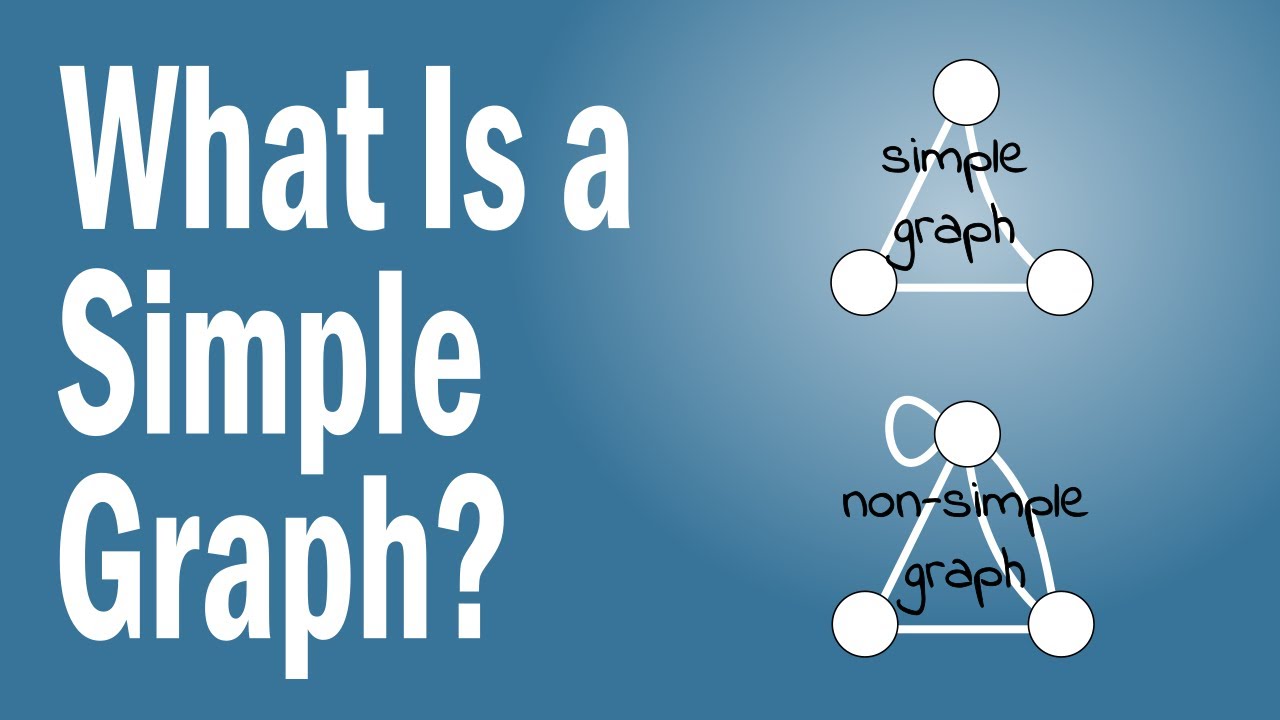
How to determine if a graph is simple. Can its degree be $1$? A graph may be tested in the wolfram language to see if it is a simple graph using simplegraphq [ g ]. A graph with no loops, but possibly with multiple edges is a multigraph.

Add edges to a graph to create an euler circuit if one doesn’t exist. Assign red color to the source vertex (putting into set u). To sum up, a simple graph is a collection of vertices and any edges that may connect them, such that every edge connects two vertices with no loops and no two vertices are joined by more than one edge.

If one graph is planar, is the other graph also planar? We can keep on reiterating to get. When a planar graph is drawn in this way, it divides the plane into regions called faces.

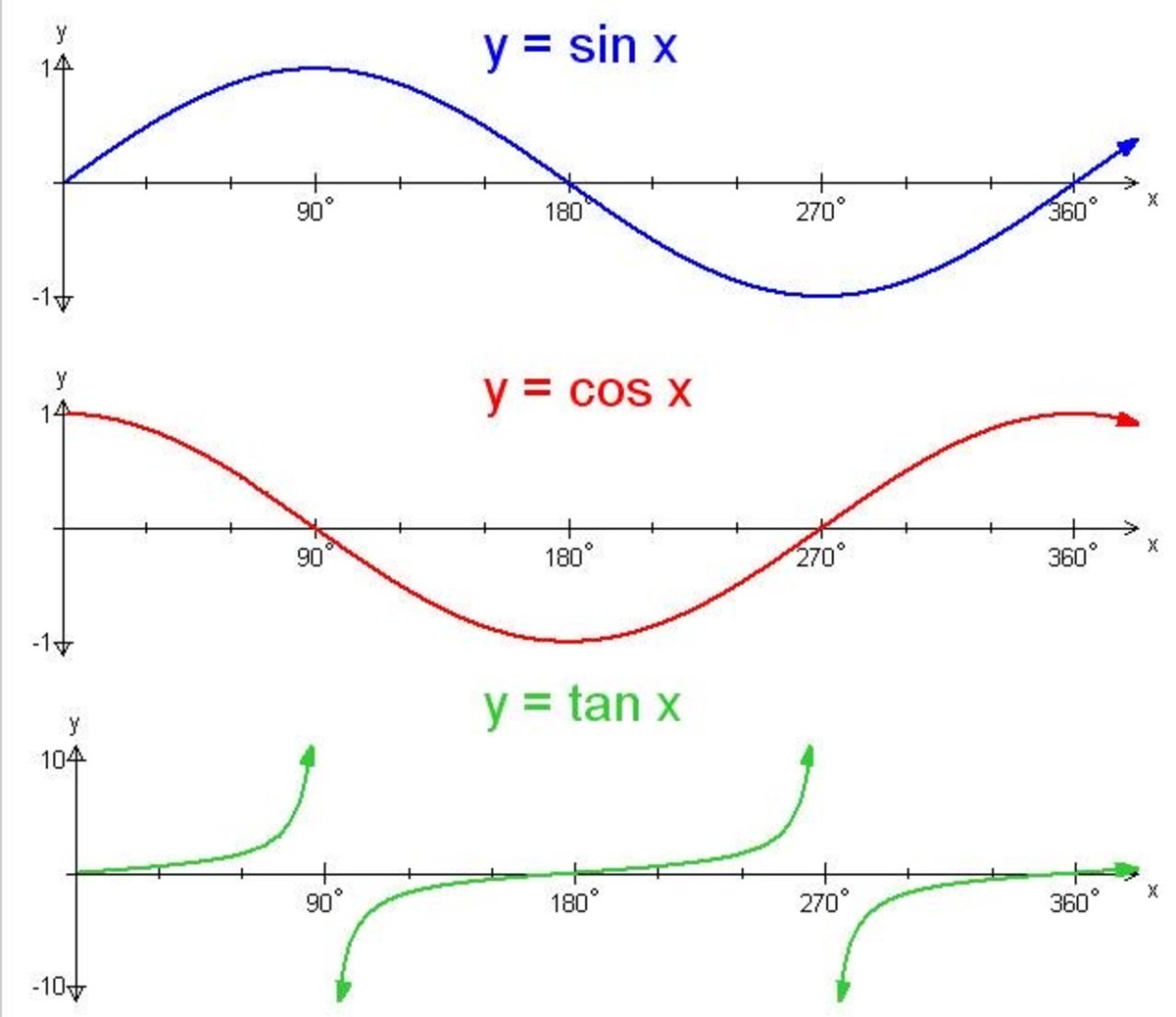
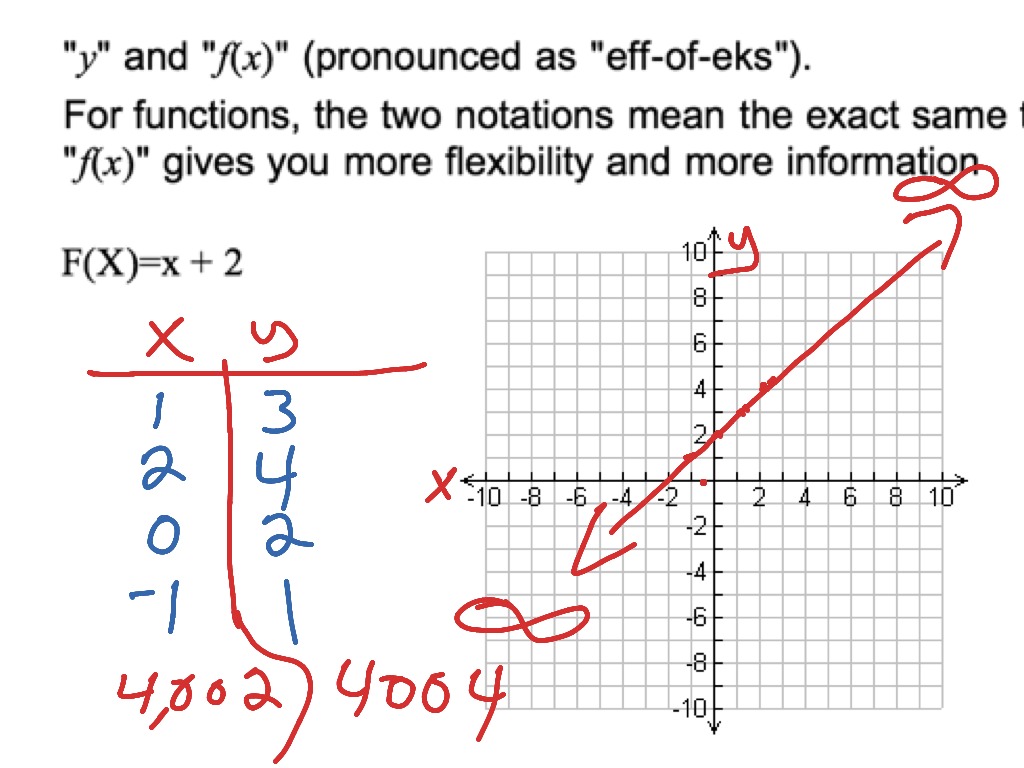
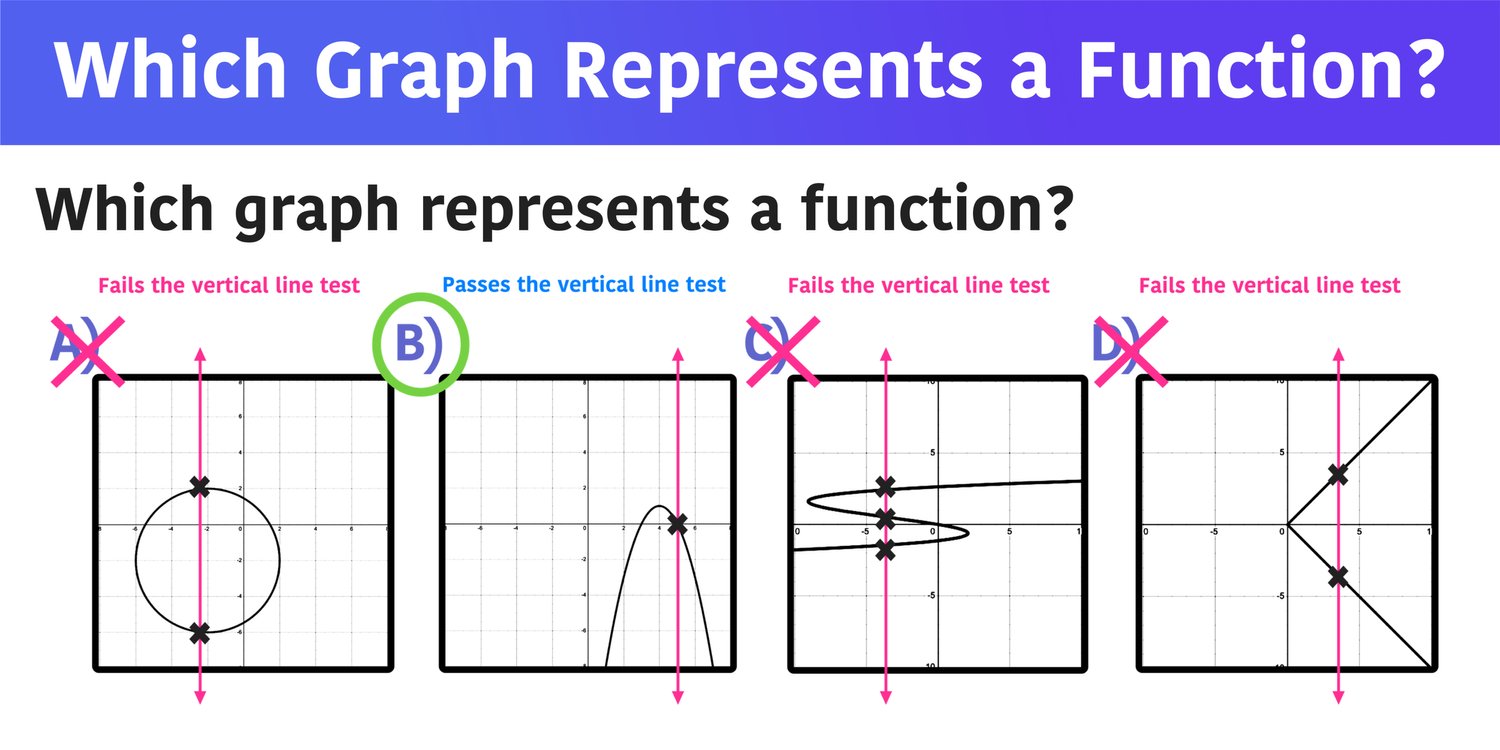
The same is true of $v_2$. Unlock the secrets of identifying functions from graphs. When a connected graph can be drawn without any edges crossing, it is called planar.

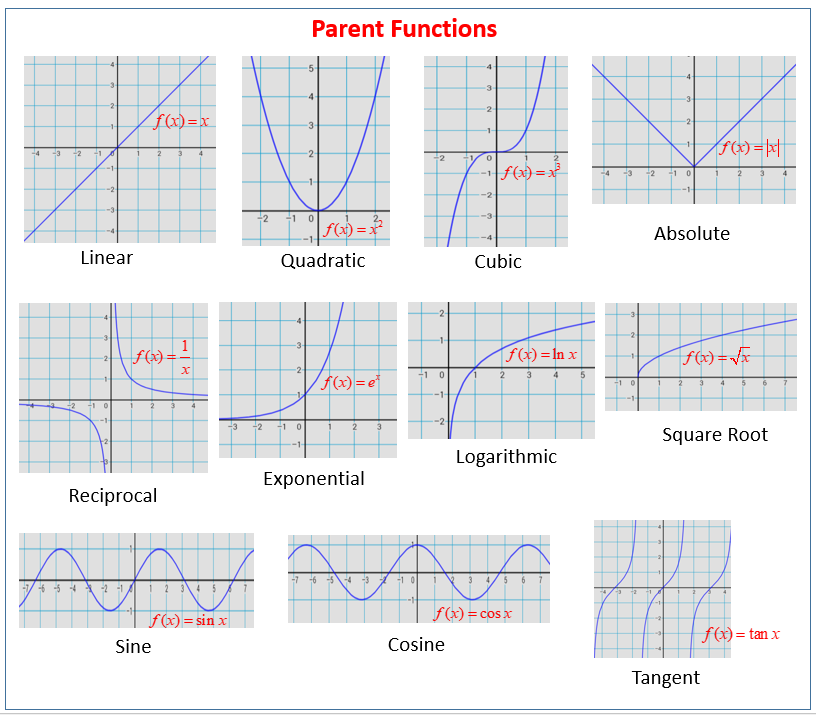
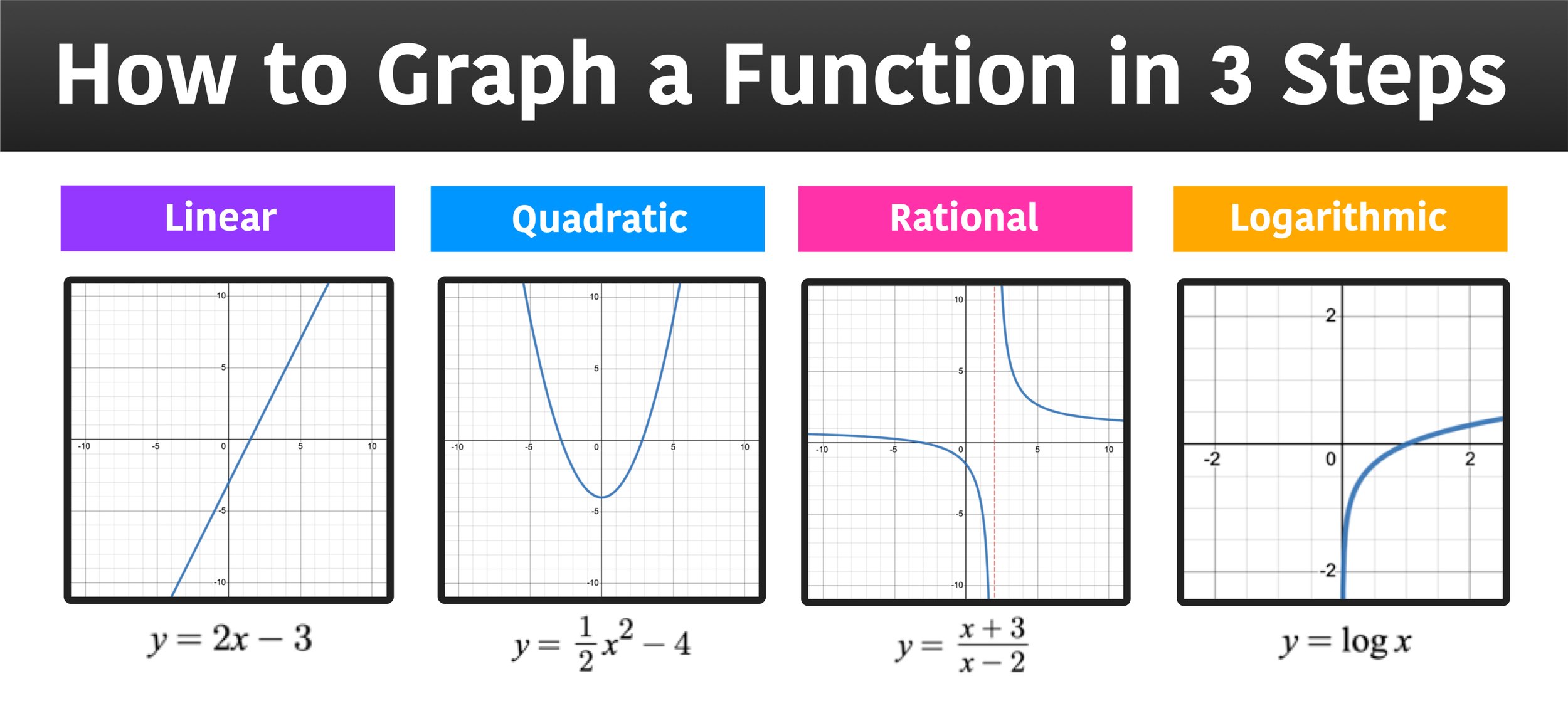
The video contains an example and exercises to practice this.d. To sum up, a simple graph is a collection of vertices and any edges that may connect them, such that every edge connects two vertices with no loops and no two vertices are joined by more than one edge. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more.

Is the number of vertices and edges in one graph the same as in the other? (2) that enumerates the number of distinct graphs with nodes (where is the number of graphs on nodes with edges) can be found using a rather complicated application of the pólya enumeration theorem. A graph with no loops and no multiple edges is a simple graph.

Explore math with our beautiful, free online graphing calculator. I once set it as a homework question. A simple graph is a graph that does not have more than one edge between any two vertices and no edge starts and ends at the same vertex.

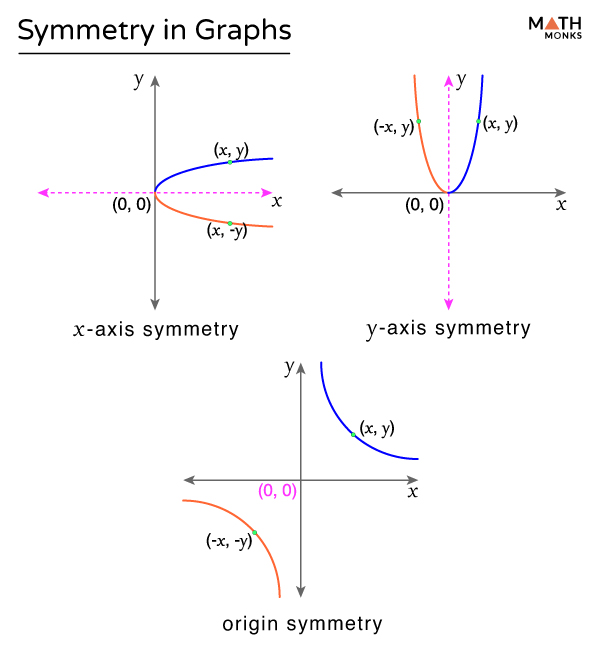
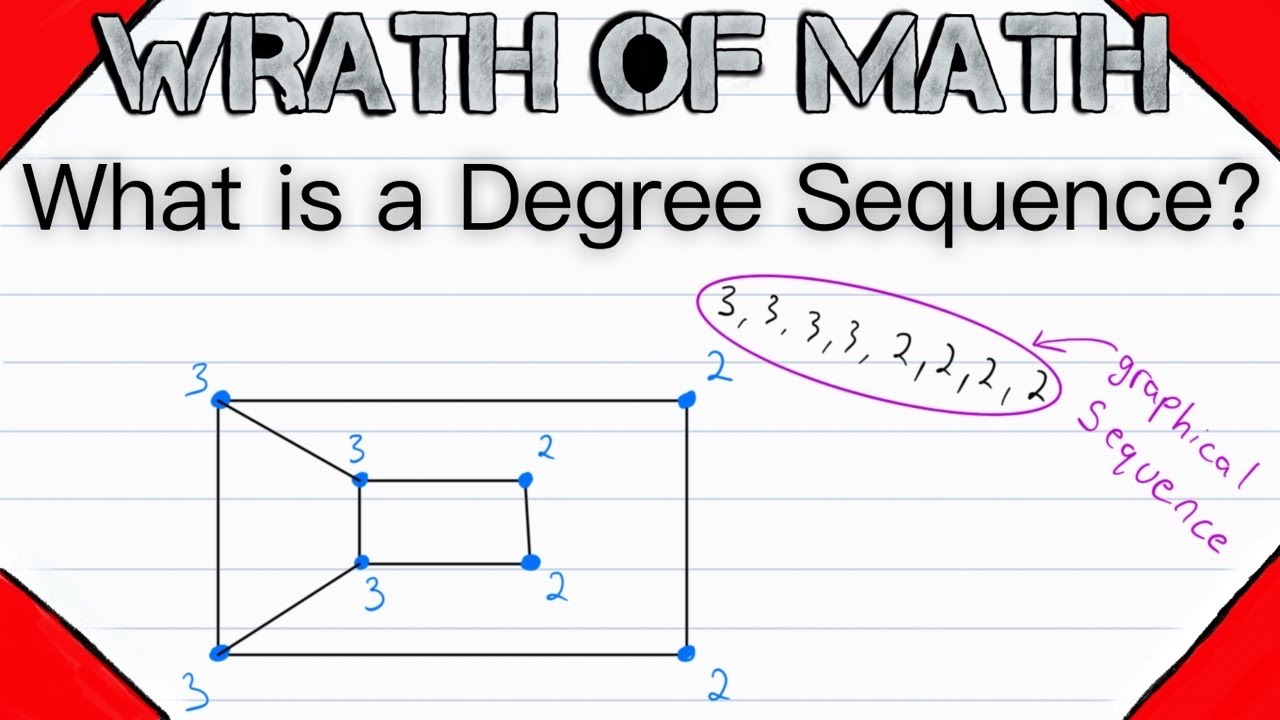
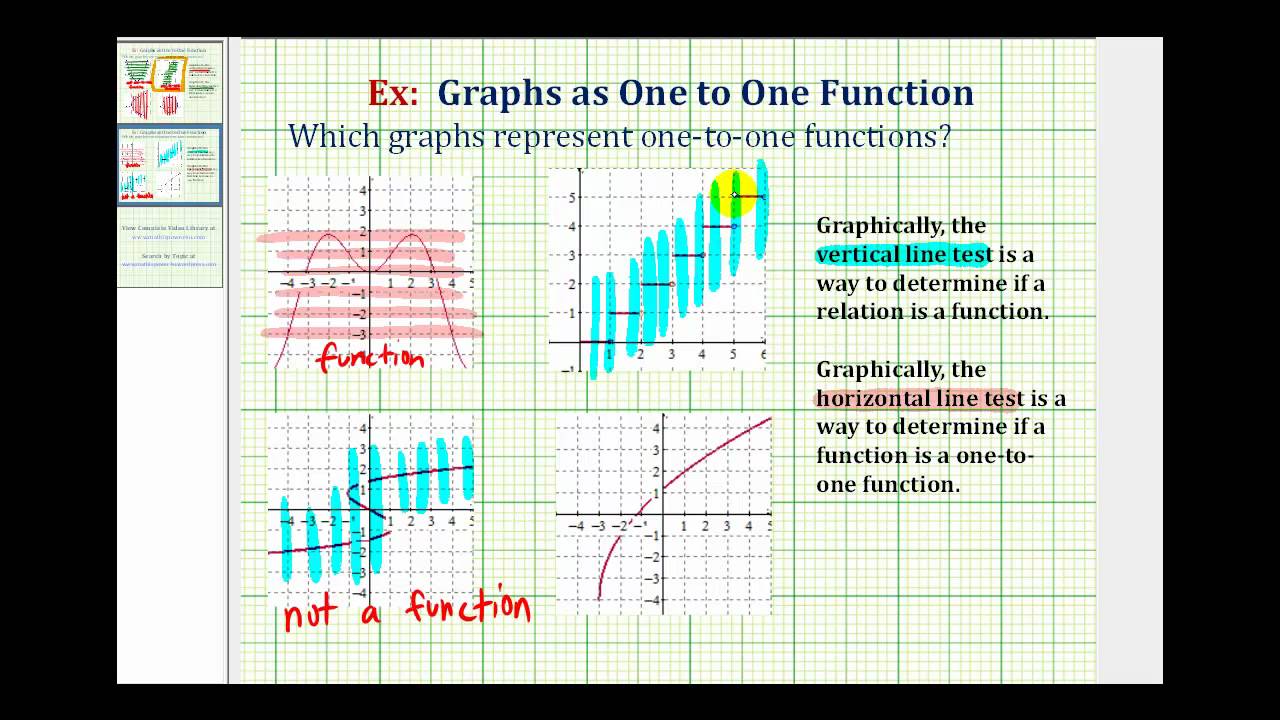
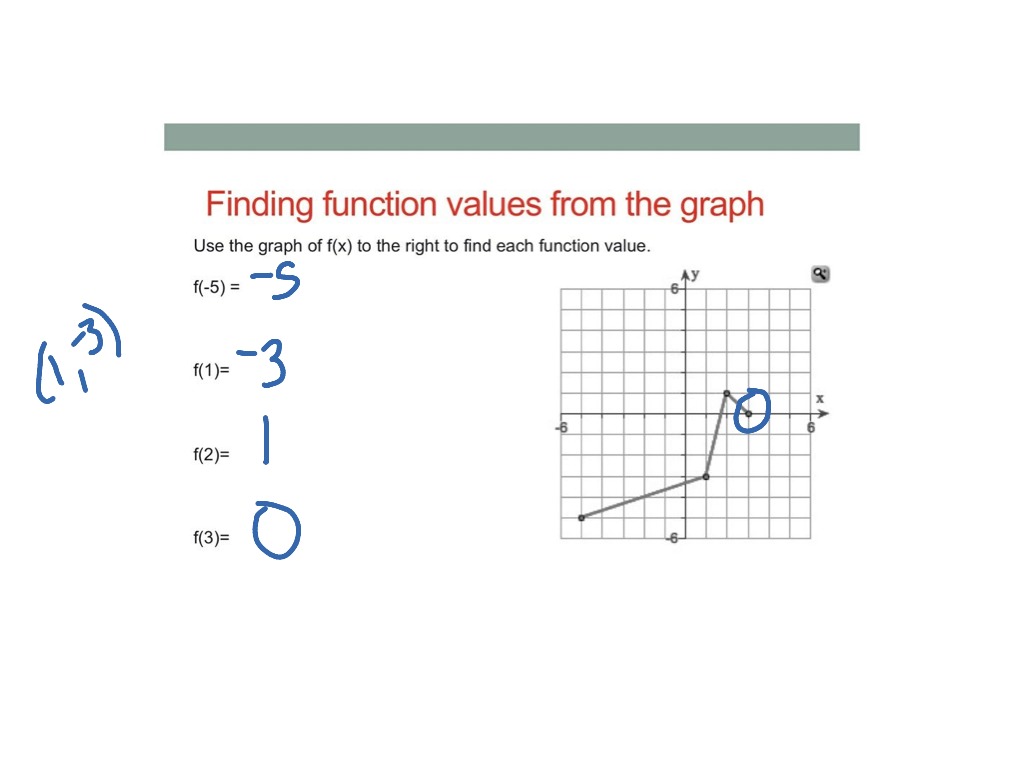
The sum $e+f$ of two such subset $e$ and $f$ is the set of edges in $e$ or $f$ but not both and scaler multiplication is defined by $1\cdot e = e$ and $0. Order the degree sequence into descending order, like 3 2 2 1. Determine whether the points on this graph represent a function.

It is stated by wikipedia as: Color all neighbor’s neighbor with red color (putting into set u). Applying this theorem, we note that the original degree sequence is graphical if and only if the degree sequence given by {7, 7, 7, 5, 4, 3, 3, 2, 1} { 7, 7, 7, 5, 4, 3, 3, 2, 1 } is graphical.

Identify whether a graph has a hamiltonian circuit or path. Two essential concepts in graph theory are graph isomorphisms and connectivity. Graph isomorphisms help determine if two graphs are structurally identical, while connectivity measures the degree to which the vertices of a graph are connected.