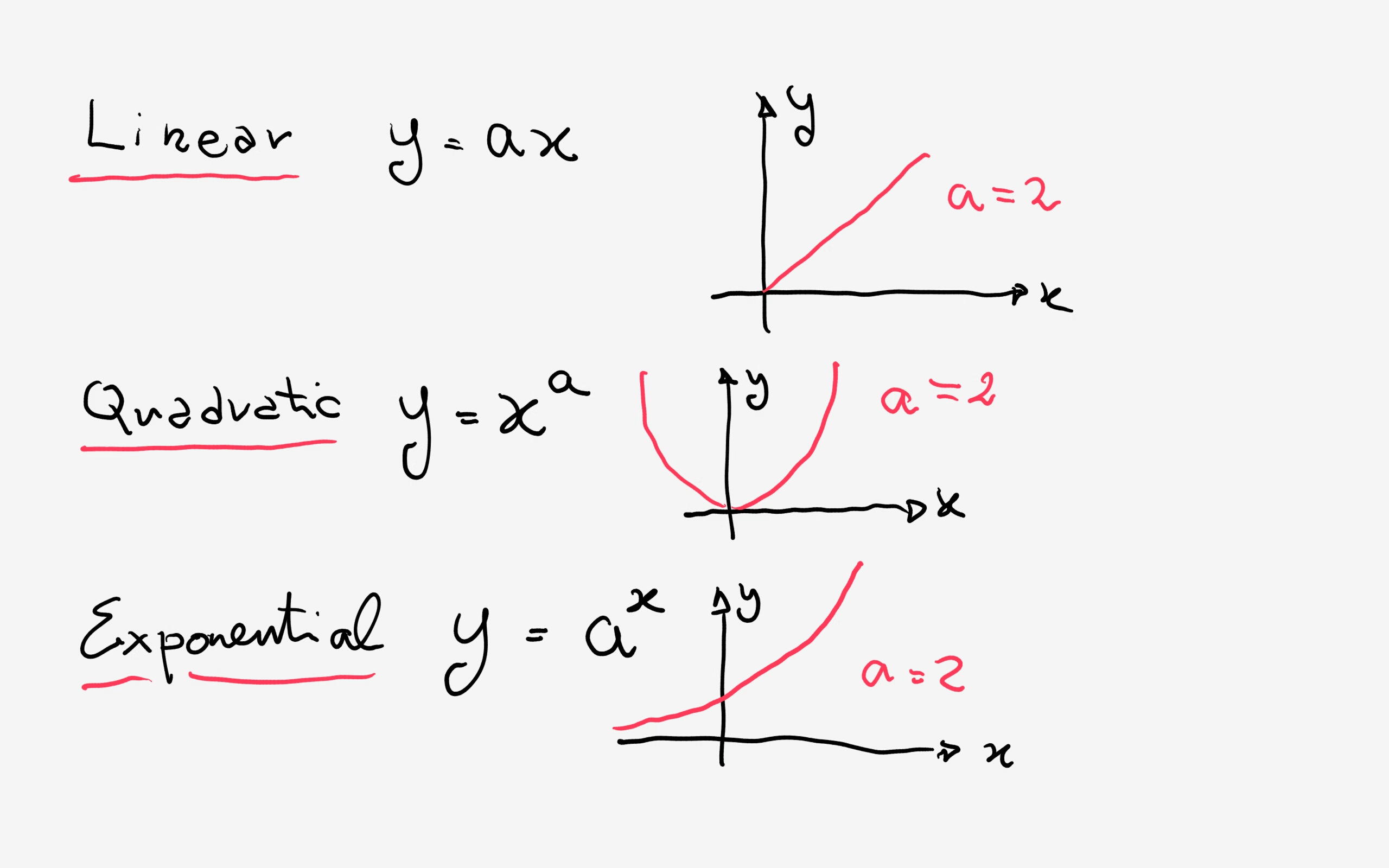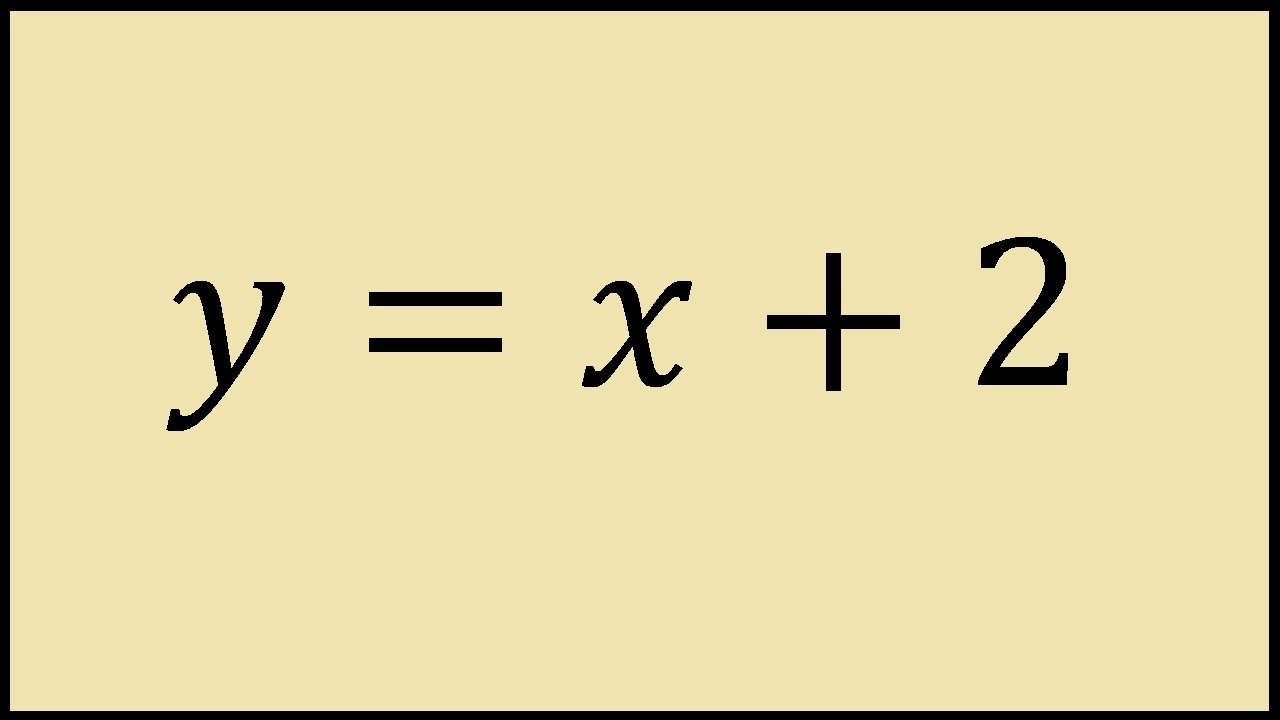Ideal Tips About How Is Y X 2 A Function To Make Log Graph On Excel

A quick check you can.

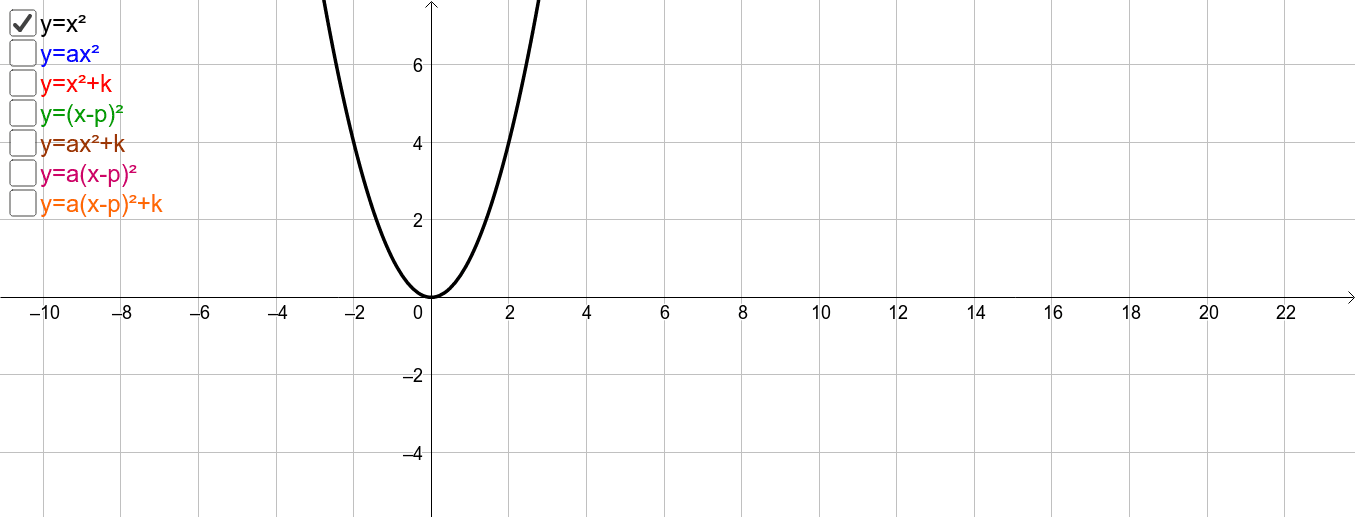
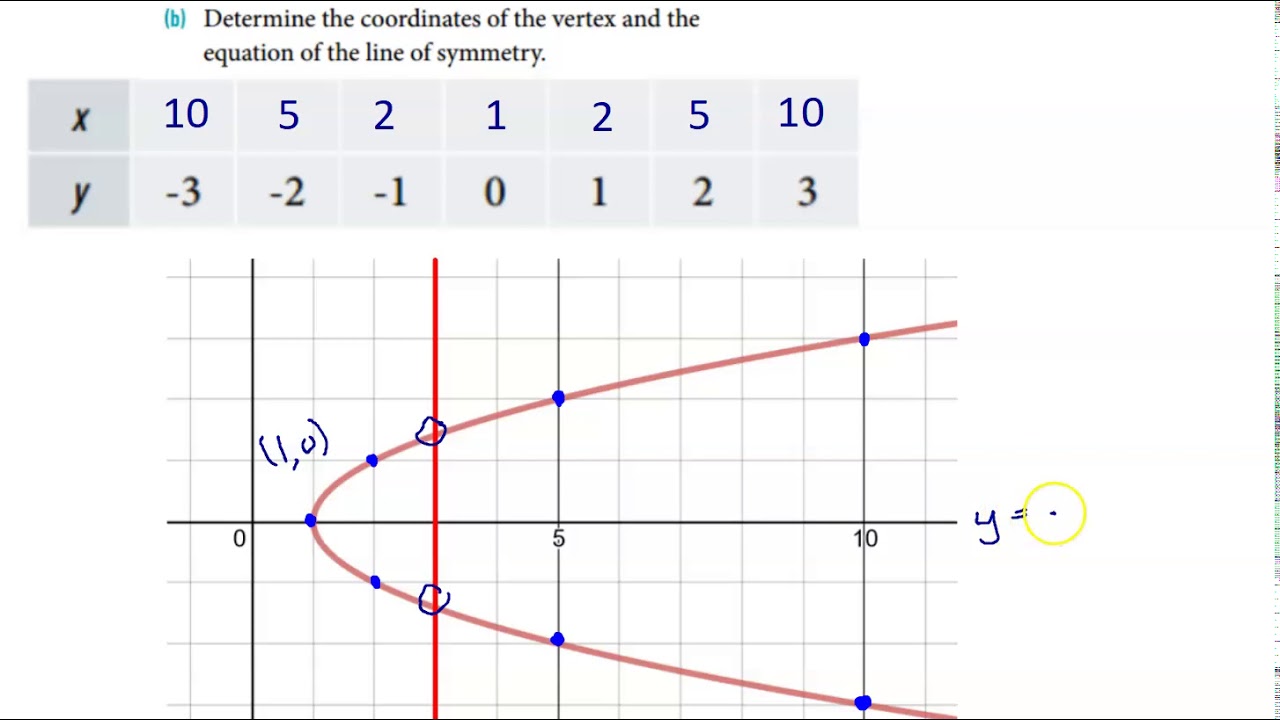
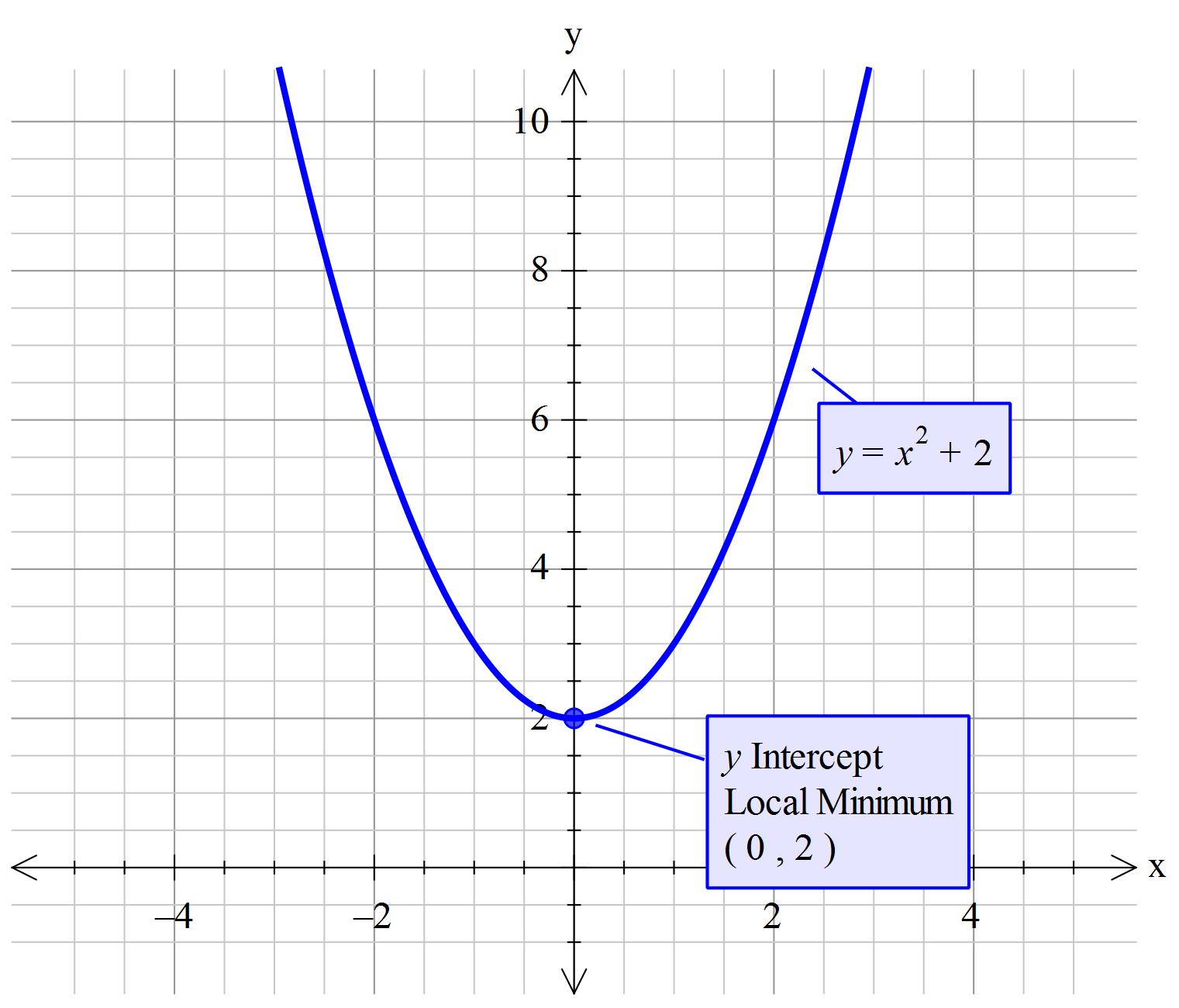
How is y x 2 a function. Yes, y is often a function of x. Y = x2 y = x 2. The value of coefficients for y=x2 are α=1, β=0 and c=0.

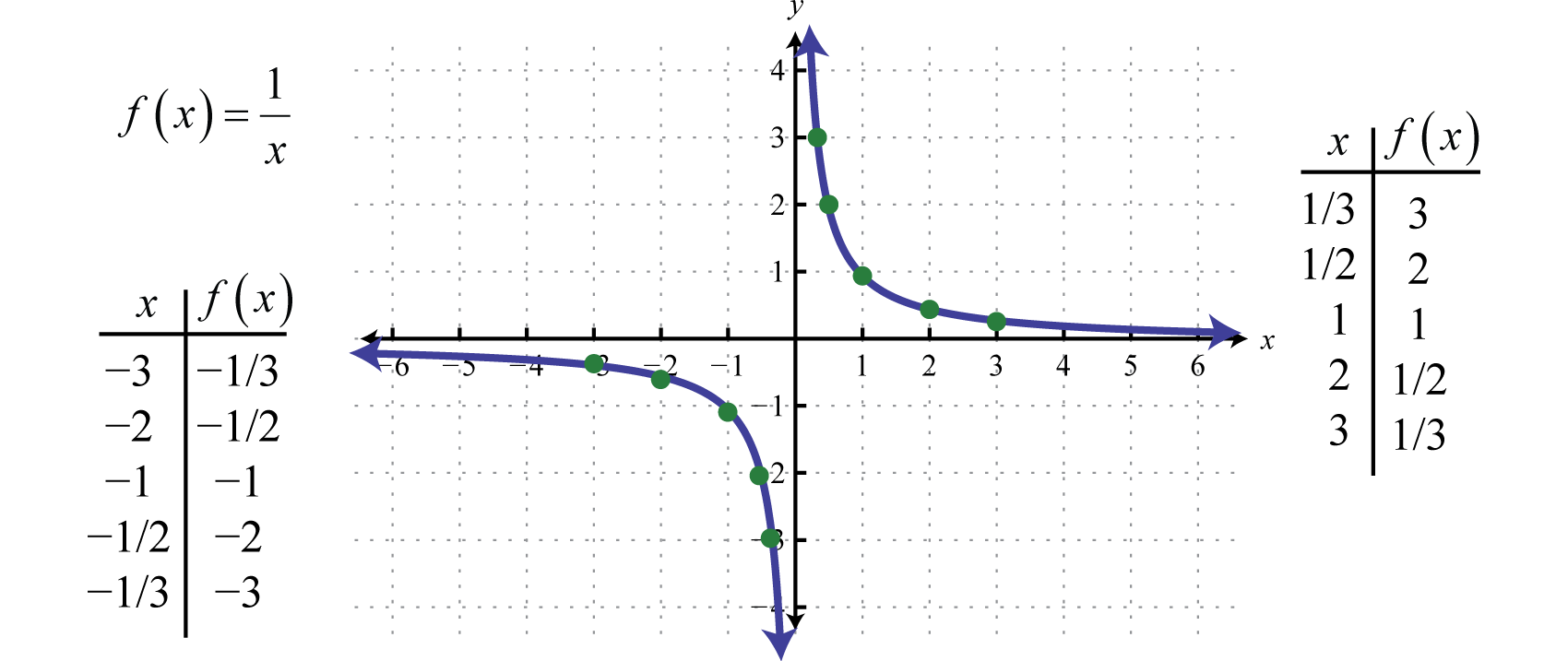
A function is a relation for which each value from the set the first components of the ordered pairs is associated with exactly one value from the set of. Take the relationship y = x^2 y can be a function of x because every x value has only one y value. Since x2 = y then x = ± √y.

X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Explore math with our beautiful, free online graphing calculator. The next step is to determine the axis of symmetry.

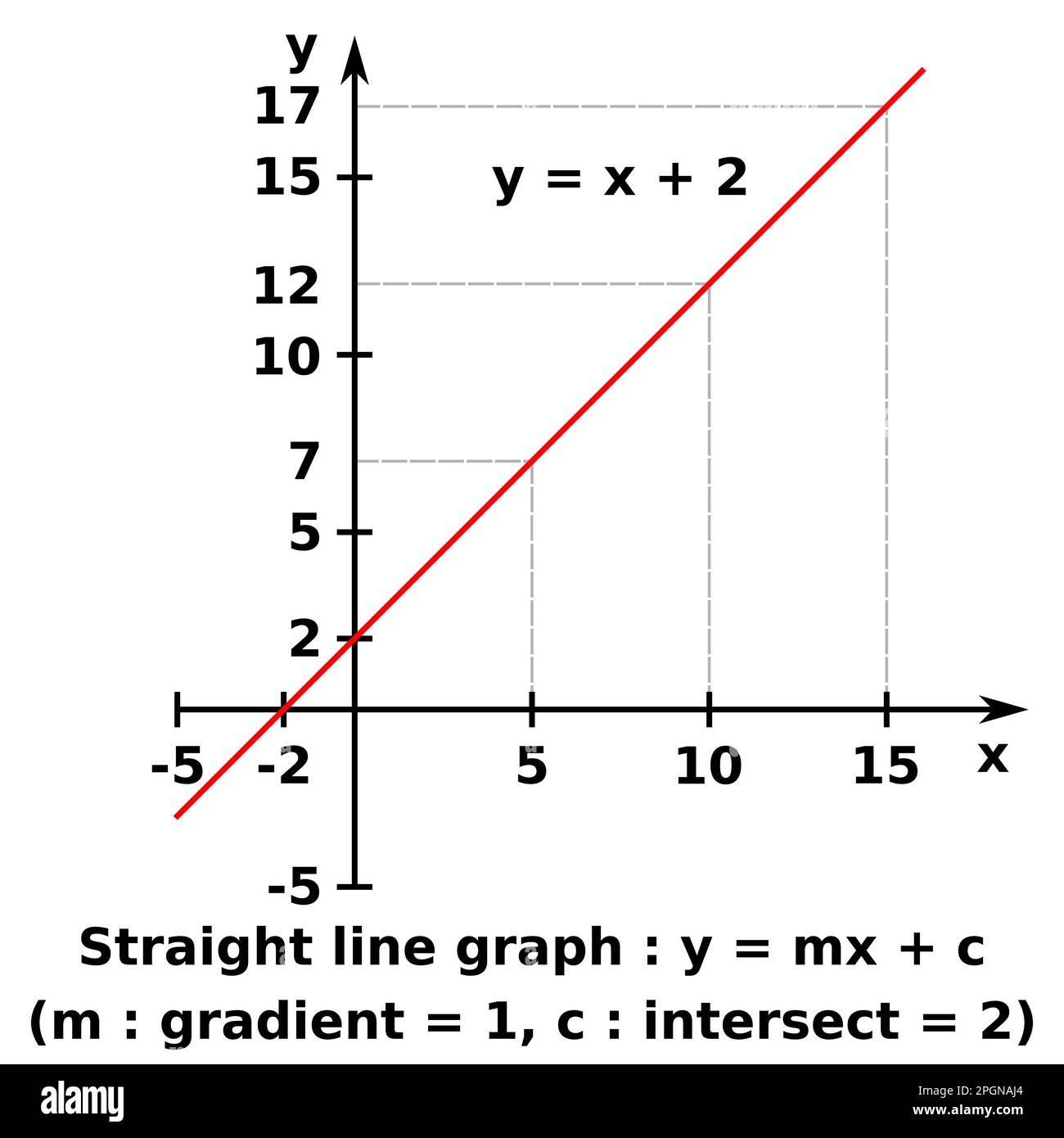
( remember 'b' can either be positive. A relation is any set of ordered pairs,(x,y).(x,y). In y = x², for every value of x, there is only one value for y.

F(x, y, z)dv where v is the a. We study an anisotropic cubic dirac semimetal subjected to a constant magnetic field. A function relates an input to an output.

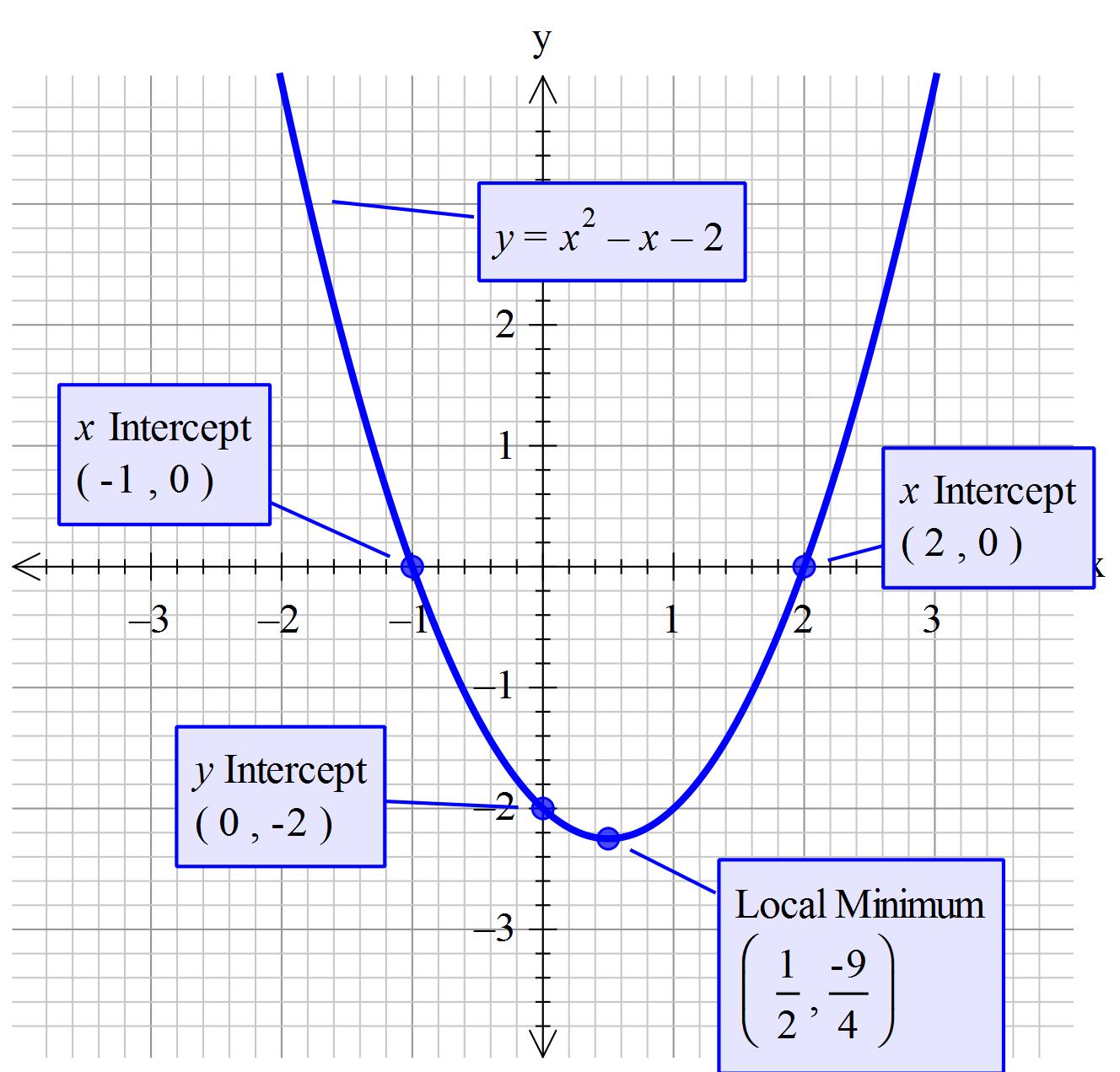
X2 +y2 = 4 = 22 looks like this: The first step is to write the equation in the form y=αx2+βx+c and determine the value of coefficients α,β and c. Equations in the form of ax2 +by2 = r2 form circles.

Thus, f −1(x) = ± √x. And the output is related somehow to the input. Given an orlicz space $ l^2 \subseteq x \subseteq l^1$ on $[0,1]$, with submultiplicative young function ${\mathrm{y}_x}$, we fully characterize the.

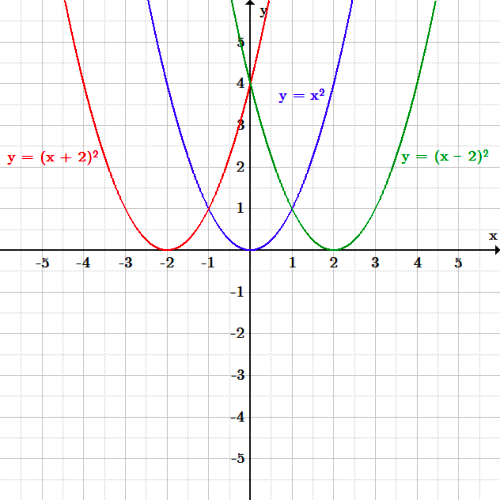
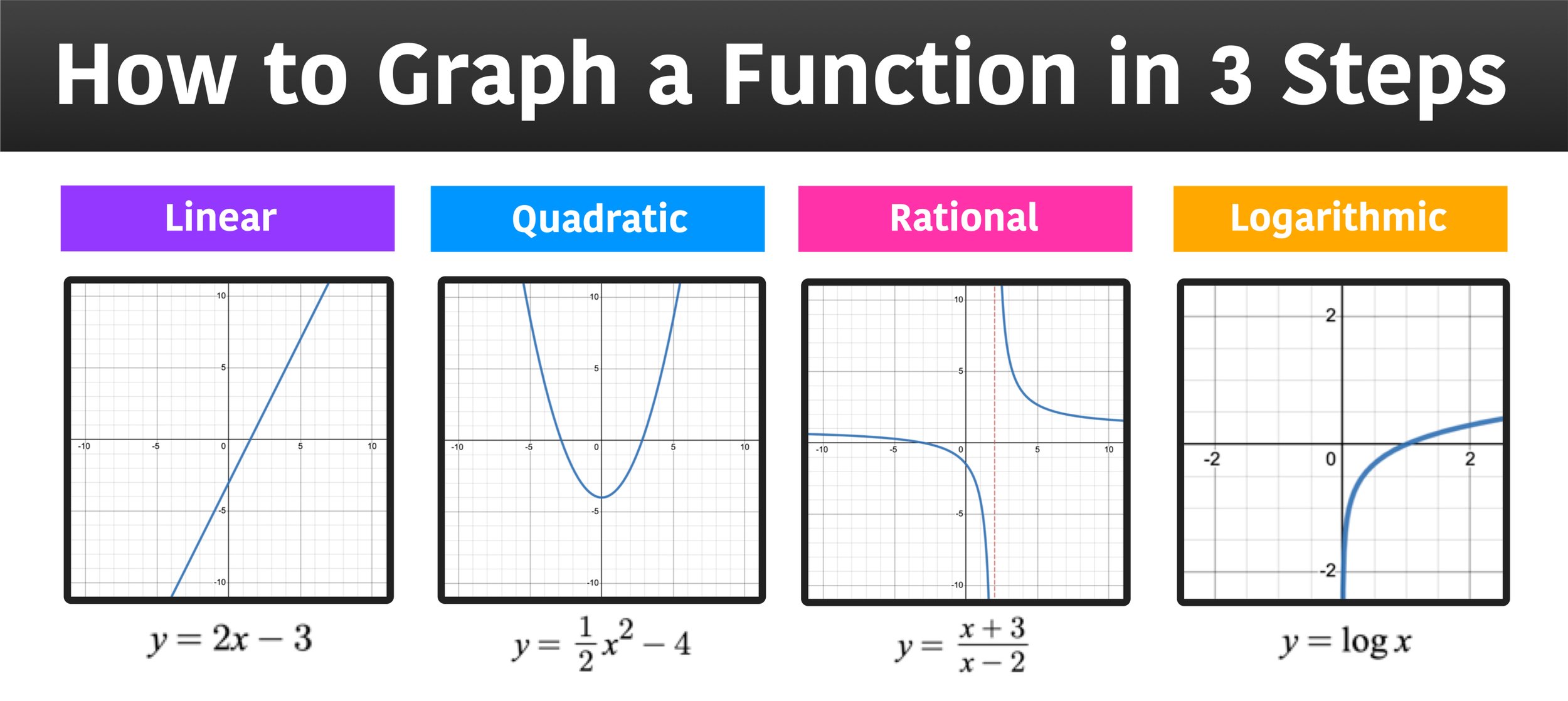
Y = x2 is arguably the simplest standard quadratic function. Find the properties of the given parabola. We can graph the function by plotting points but it is probably more enlightening to consider a few.

(0, 1 4) ( 0, 1 4) axis of. But x could not be a function of y, because each positive y has two x values. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more.

The graph of the y=x2can be drawn by following the steps mentioned below. The average value of a function over a solid is given by volume of the region q. Yes it is.